Hướng dẫn giải Đề kiểm tra học kì 2 Toán 10 – Đề số 1 – Cánh diều – Đề thi học kì 2 – Đề thi đề kiểm tra Toán lớp 10 Cánh diều. I. PHẦN TRẮC NGHIỆM ( 35 câu – 7,0 điểm )….
Đề thi:
PHẦN I: TRẮC NGHIỆM ( 35 câu – 7 điểm)
Câu 1: Bạn A có 7 cái bút chì và 8 cái bút mực. Hỏi có bao nhiêu cách để bạn An chọn một chiếc bút?
A. 15. B. 7 C. 8. D. 56.
Câu 2: Cho 6 chữ số 2, 3, 4, 5, 6, 7. Hỏi có bao nhiêu số tự nhiên gồm 3 chữ số được lập thành từ 6 chữ số đó
A. 36. B. 18. C. 256 D. 216.
Câu 3: Xếp 7 người vào một băng ghế dài có 9 chỗ. Hỏi có bao nhiêu cách xếp?
A. 36. B. 5040. C. 181440. D. 2250.
Câu 4: Có 6 quyển sách toán, 5 quyển sách hóa và 3 quyển sách lí (các quyển sách đều khác nhau) Hỏi có bao nhiêu cách xếp 14 quyển sách trên thành một hàng dài lên giá sách sao cho các quyển sách cùng loại được xếp cạnh nhau?
A. 518400. B. 3110400. C. 86400. D. 46800.
Câu 5: Có 12 quyển sách khác nhau. Chọn ra 5 cuốn, hỏi có bao nhiêu cách?
A. 95040. B. 792. C. 120. D. 5040.
Câu 6: Có 30 câu hỏi khác nhau gồm 5 câu khó, 10 câu TB, 15 câu dễ. Từ 30 câu đó lập được bao nhiêu đề, mỗi đề gồm 5 câu hỏi khác nhau trong đó phải có đủ cả 3 loại câu hỏi và số câu dễ không ít hơn 2.
A. 85631. B. 56875. C. 34125. D. 22750.
Câu 7: Trong các phát biểu sau, phát biểu nào sai?
A. \({\left( {a + b} \right)^4} = {a^4} + 4{a^3}b + 6{a^2}{b^2} + 4a{b^3} + {b^4}\).
B. \({\left( {a – b} \right)^4} = {a^4} – 4{a^3}b + 6{a^2}{b^2} – 4a{b^3} + {b^4}\).
C. \({\left( {a + b} \right)^4} = {b^4} + 4{b^3}a + 6{b^2}{a^2} + 4b{a^3} + {a^4}\).
D. \({\left( {a + b} \right)^4} = {a^4} + {b^{4.}}\).
Câu 8: Hệ số của \({x^3}\)trong khai triển biểu thức \({\left( {2x – 1} \right)^4}\) là
A. 32. B. -32. C. 8. D. -8.
Câu 9: Số quy tròn của 314, 87 đến hàng đơn vị là:
A. 315. B. 314,9. C. 310. D. 314.
Câu 10: Cho mẫu số liệu: 1 3 6 8 9 12. Số trung bình cộng của mẫu số liệu là:
A. 6. B. 9. C. 7. D. 6,5.
Câu 11: Điểm kiểm tra 15 phút môn Toán của 9 bạn tổ 1 như sau:
6 ; 7,3; 8; 6; 7,5; 9; 9; 8,7; 8,5
Tứ phân vị của mẫu số liệu trên là:
A. \({Q_1} = 7,5;{Q_2} = 7,65;{Q_3} = 8,85\).
B. \({Q_1} = 7,65;{Q_2} = 7,5;{Q_3} = 8,85\).
C. \({Q_1} = 6,5;{Q_2} = 8;{Q_3} = 8,85\).
D. \({Q_1} = 8;{Q_2} = 6,65;{Q_3} = 8,85\).
Câu 12: Gieo lần lượt hai con súc sắc. Tính xác suất để tổng số chấm trên hai mặt bằng hoặc lớn hơn 8?
A. \(\frac{{11}}{{36}}\) B.\(\frac{1}{6}\) C. \(\frac{5}{{18}}\) D.\(\frac{5}{{12}}\)
Câu 13: Gieo một đồng xu hai lần liên tiếp, ta có không gian mẫu là:
A. \(\left\{ {S;N} \right\}\).
B. \(\left\{ {SS;NN} \right\}\).
C. \(\left\{ {SS;SN;NS;NN} \right\}\).
D. \(\left\{ {S;N;SN} \right\}\).
Câu 14: Xác xuất của biến cố A trong trò chơi tung một đồng xu hai lần liên tiếp được tính bằng công thức nào sau đây?
A. \(\frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\). B. \(\frac{{n\left( \Omega \right)}}{{n\left( A \right)}}\). C. \(\frac{A}{\Omega }\). D. \(\frac{\Omega }{A}\).
Câu 15: Gieo một xúc xắc hai lần liên tiếp. Xác suất của biến cố “ lần thứ nhất xuất hiện mặt 6 chấm” là:
A. \(\frac{1}{2}.\) B. \(\frac{1}{{36}}.\) C. \(\frac{1}{6}.\) D. \(\frac{1}{4}.\)
Câu 16: Xét một phép thử có không gian mẫu và là một biến cố của phép thử đó. Phát biểu nào dưới đây là sai?
A. Xác suất của biến cố A là số \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( P \right)}}.\)
B. \(0 \le P\left( A \right) \le 1.\)
C. \(P\left( A \right) = 0\) khi và chỉ khi là chắc chắn.
D. \(P\left( A \right) = 1 – P\left( {\overline A } \right)\).
Câu 17: Số phần tử không gian mẫu của phép thử gieo đồng thời 1 con xúc xắc và 1 đồng xu là
A. 2. B. 12. C. 8. D. 36.
Câu 18: Có 4 viên bi đỏ và 3 viên bi xanh. Lấy ngẫu nhiên 3 viên. Tính xác suất trong 3 viên có 2 viên màu đỏ.
A. \(\frac{6}{{35}}.\)
B. \(\frac{{18}}{{35}}.\)
C. \(\frac{9}{{35}}.\)
D. \(\frac{8}{{35}}.\)
Câu 19: Trong mặt phẳng Oxy, cho vecto \(\vec a = – 3\vec i + \vec j\). Tọa độ của \(\vec a\) là:
A. \(\left( {3;1} \right)\).
B. \(\left( {1;3} \right)\).
C. \(\left( {3; – 1} \right)\).
D. \(\left( { – 3;1.} \right)\)
Câu 20: Trong mặt phẳng Oxy, cho hai điểm \(A\left( {2; – 3} \right),B\left( {4;7} \right)\). Tọa độ trung điểm của đoạn thẳng AB là:
A. \(\left( {3;2} \right).\)
B. \(\left( { – 1; – 5} \right).\)
C. \(\left( {1;5} \right)\).
D. \(\left( {2;3} \right).\)
Câu 21: Cho tam giác ABC có \(A\left( {2;6} \right),B\left( { – 2;2} \right),C\left( {8;0} \right)\). Tam giác ABC là:
A. Tam giác đều.
B. Tam giác cân tại A
C. Tam giác vuông tại A
D. Tam giác vuông cân tại A
Câu 22: Trong mặt phẳng \(Oxy,\) cho đường thẳng \(d:\,\,3x – 2y + 5 = 0.\) Vectơ nào dưới đây là một vectơ pháp tuyến của \(d\,?\)
A. \(\vec n = \left( {3;\,2} \right).\)
B. \(\vec n = \left( {3;\, – 2} \right).\)
C. \(\vec n = \left( {2;\,3} \right).\)
D. \(\vec n = \left( { – 2;\,3} \right).\)
Câu 23: Viết phương trình tham số của đường thẳng đi qua hai điểm và .
A. \(\left\{ \begin{array}{l}x = 1 + 2t\\y = 3 + t\end{array} \right.\)
B.\(\left\{ \begin{array}{l}x = – 1 – 2t\\y = 3 – t\end{array} \right.\)
C. \(\left\{ \begin{array}{l}x = 3 + 2t\\y = – 1 + t\end{array} \right.\)
D. \(\left\{ \begin{array}{l}x = – 1 – 2t\\y = 3 + t\end{array} \right.\)
Câu 24: Xét vị trí tương đối của hai đường thẳng \({d_1}:x – 2y + 1 = 0\)và \({d_2}: – 3x + 6y – 10 = 0\).
A. Song song.
B. Trùng nhau.
C. Vuông góc với nhau.
D. Cắt nhau nhưng không vuông góc nhau.
Câu 25: Cho đường thẳng và . Tính cosin của góc tạo bởi hai đường thẳng đã cho.
A. \(\frac{{3\sqrt {10} }}{{10}}\)
B. \(\frac{3}{5}\)
C. \(\frac{{\sqrt {10} }}{{10}}\)
D. \(\frac{3}{{10}}\)
Câu 26: Tọa độ độ tâm I và bán kính R của đường tròn \((C):{(x – 1)^2} + {(y + 3)^2} = 16\) là:
A. I( – 1;3),R = 4
B. I(1; – 3),R = 4
C. I(1; – 3),R = 16
D. I( – 1;3),R = 16
Câu 27: Đường tròn có tâm và bán kính lần lượt là:
A. \(I(3; – 1),R = 4\)
B.\(I( – 3;1),R = 4\)
C. \(I(3; – 1),R = 2\)
D. \(I( – 3;1),R = 2\)
Câu 28: Đường tròn đường kính với có phương trình là:
A. \({\left( {x – 2} \right)^2} + {(y – 3)^2} = 5\)
B. \({\left( {x + 1} \right)^2} + {(y + 2)^2} = 17\)
C. \({\left( {x – 2} \right)^2} + {(y + 3)^2} = \sqrt 5 \)
D. \({\left( {x – 2} \right)^2} + {(y + 3)^2} = 5\)
Câu 29: Elip có độ dài trục lớn là 10 và có một tiêu điểm . Phương trình chính tắc của elip là:
A. \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\)
B. \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{16}} = 1\)
C. \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{81}} = 1\)
D. \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\)
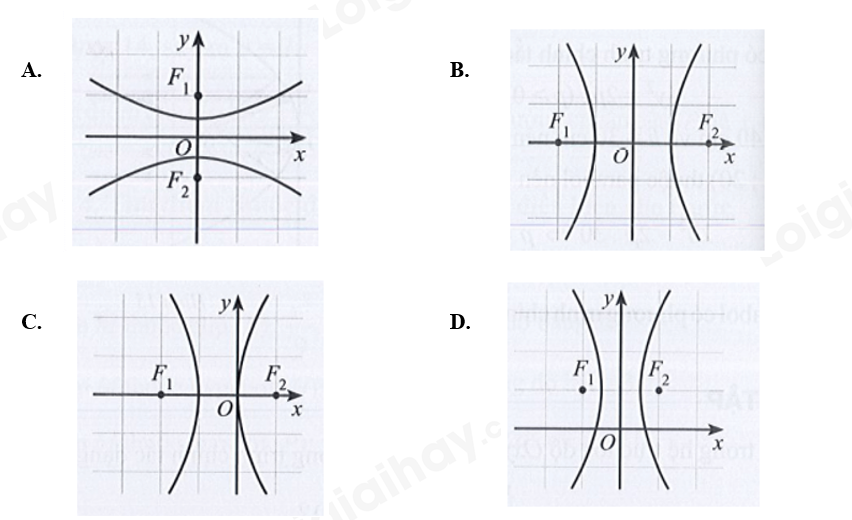
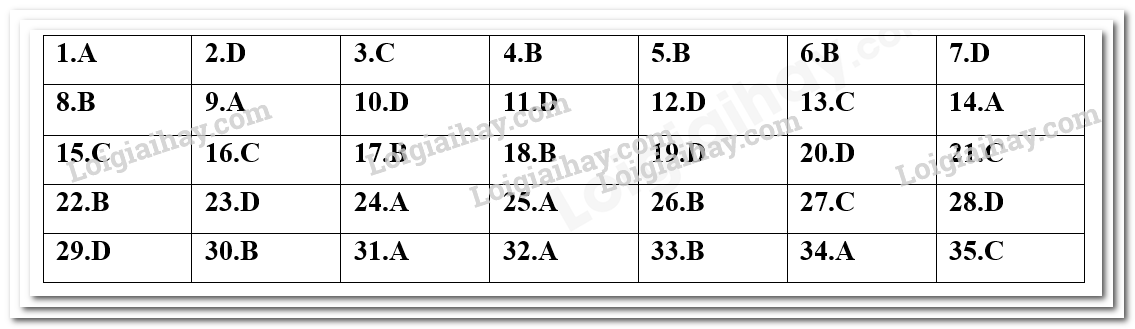
Câu 30: Hyperbol trong hệ trục tọa độ Oxy nào dưới đây có phương trình chính tắc dạng \(\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} = 1\left( {a > 0,b > 0} \right)\)?
Câu 31: Parabol (P) có phương trình đường chuẩn là \(x + \frac{1}{4} = 0\). Phương trình chính tắc của (P) là:
A. \({y^2} = \frac{1}{2}x.\)
B. \({y^2} = 2x\).
C. \({y^2} = x.\)
D. \({y^2} = 4x.\)
Câu 32: Hệ số lớn nhất trong khai triển biểu thức \({\left( {x + 1} \right)^5}\)là:
A. 10. B. 5.
C. 6. D. 4.
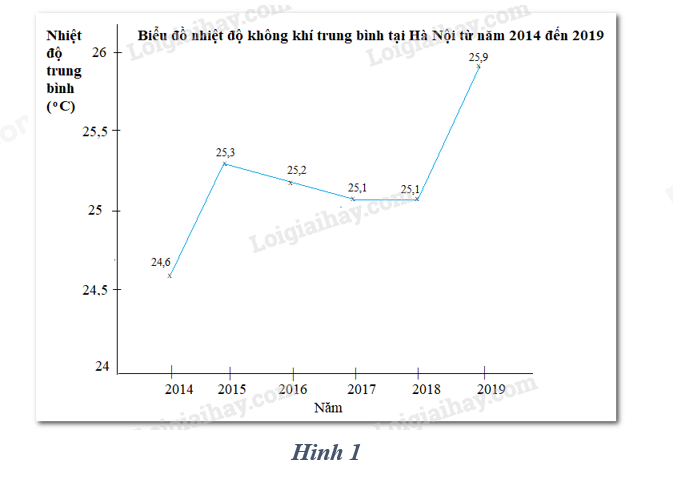
Biểu đồ ở hình 1 biểu diễn nhiệt độ không khí tại Hà Nội giai đoạn 2014 – 2019. Sử dụng mẫu số liệu từ biểu đồ này để hoàn thành các câu 34, 34, 35.
Câu 33: Khoảng biến thiên của mẫu số liệu là:
A. 1. B. 1,3. C. 50,5. D. 0,65.
Câu 34: Khoảng tứ phân vị của mẫu số liệu là:
A. 0,2. B. 0,15. C. 25,15. D. 0,05.
Câu 35: Phương sai của mẫu số liệu gần nhất với số nào sau đây:
A. 0,1. B. 0,15. C. 0,147. D. 1.
PHẦN II: TỰ LUẬN ( 2 câu – 3 điểm)
Câu 36: a) (1.0 điểm) Giả sử hệ số của x trong khai triển biểu thức \({\left( {ax + \frac{1}{x}} \right)^5}\) bằng 270. Tìm giá trị của a.
b) (0.5 điểm) Tìm số đường chéo của 1 đa giác lồi có 10 cạnh.
Câu 37: a) (1.0 điểm ) Cho tam giác ABC có phương trình các đường thẳng \(AB:2x – 3y – 1 = 0;\)
\(BC:x + 3y + 7 = 0;\) \(CA:5x – 2y + 1 = 0\). Viết phương trình tổng quát của đường cao kẻ từ \(B.\)
b) (0.5 điểm) Cho tam giác ABC với \(A\left( { – 1;0} \right),B\left( {2;3} \right),C\left( {3; – 6} \right)\) và đường thẳng \(d:x – 2y – 3 = 0\). Tìm điểm M trên d sao cho \(\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right|\) nhỏ nhất.
Đáp án Đề thi:
HƯỚNG DẪN GIẢI CHI TIẾT
THỰC HIỆN: BAN CHYÊN MÔN GiaiBaitapsgk.COM
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm).
Câu 1: Bạn A có 7 cái bút chì và 8 cái bút mực. Hỏi có bao nhiêu cách để bạn An chọn một chiếc bút?
A. 15. B. 7 C. 8. D. 56.
Phương pháp
Áp dụng quy tắc cộng
Giải
Chọn A
– TH1: chọn 1 bút chì trong số 7 bút chì: 7 cách
– TH2: chọn 1 bút mực trong số 8 bút mực: 8 cách
Theo qt cộng có: 7+8=15 cách thỏe đề
Câu 2: Cho 6 chữ số 2, 3, 4, 5, 6, 7. Hỏi có bao nhiêu số tự nhiên gồm 3 chữ số được lập thành từ 6 chữ số đó
A. 36. B. 18. C. 256 D. 216.
Phương pháp
Áp dụng quy tắc nhân
Giải
Chọn D
Gọi số cần lập là \(\overline {abc} \).
– B1: chọn 1 chữ số cho a: 6 cách
– B2: chọn 1 chữ số cho b: 6 cách
– B3: chọn 1 chữ số cho c: 6 cách
Theo qt nhân, có \({6^3} = 216\) số thỏa đề.
Câu 3: Xếp 7 người vào một băng ghế dài có 9 chỗ. Hỏi có bao nhiêu cách xếp?
A. 36. B. 5040. C. 181440. D. 2250.
Phương pháp
Số tổ hợp chập k của n phần tử là \(C_n^k = \frac{{n!}}{{\left( {n – k} \right)!k!}}\)
Giải
Chọn C
– B1: chọn 7 ghế từ 9 ghế: \(C_9^7\) cách
– B2: sắp xếp 7 người vào 7 ghế đã chọn: 7! Cách
Vậy có 7!.\(C_9^7\)= 181440 cách thỏa đề
Câu 4: Có 6 quyển sách toán, 5 quyển sách hóa và 3 quyển sách lí (các quyển sách đều khác nhau) Hỏi có bao nhiêu cách xếp 14 quyển sách trên thành một hàng dài lên giá sách sao cho các quyển sách cùng loại được xếp cạnh nhau?
A. 518400. B. 3110400. C. 86400. D. 46800.
Phương pháp
Áp dụng công thức hoán vị
Giải
Chọn B
– Xếp 6 quyển toán thành một hàng: 6! Cách
– Xếp 5 quyển hóa thành một hàng: 5! Cách
– Xếp 3 quyển lí thành một hàng: 3! Cách
– Hoán đổi vị trí 3 nhóm trên: 3! Cách
Vậy có 6!.5!.3!.3! = 3110400 cách
Câu 5: Có 12 quyển sách khác nhau. Chọn ra 5 quyển, hỏi có bao nhiêu cách?
A. 95040. B. 792. C. 120. D. 5040.
Phương pháp
Số tổ hợp chập k của n phần tử là \(C_n^k = \frac{{n!}}{{\left( {n – k} \right)!k!}}\)
Giải
Chọn B
Có \(C_{12}^5 = 792\)cách
Câu 6: Có 30 câu hỏi khác nhau gồm 5 câu khó, 10 câu TB, 15 câu dễ. Từ 30 câu đó lập được bao nhiêu đề, mỗi đề gồm 5 câu hỏi khác nhau trong đó phải có đủ cả 3 loại câu hỏi và số câu dễ không ít hơn 2.
A. 85631. B. 56875. C. 34125. D. 22750.
Phương pháp
Số tổ hợp chập k của n phần tử là \(C_n^k = \frac{{n!}}{{\left( {n – k} \right)!k!}}\)
Giải
Chọn B
– TH1: 2 câu dễ + 1 câu TB + 2 câu khó: \(C_{15}^2.C_{10}^1.C_5^2 = 10500\)cách
– TH2: 2 câu dễ + 2 câu TB + 1 câu khó: \(C_{15}^2.C_{10}^2.C_5^1 = 23625\)cách
– TH3: 3 câu dễ + 1 câu TB + 1 câu khó: \(C_{15}^3.C_{10}^1.C_5^1 = 22750\)cách
Vậy có 10500+23625+22750 = 56875 cách
Câu 7: Trong các phát biểu sau, phát biểu nào sai?
A. \({\left( {a + b} \right)^4} = {a^4} + 4{a^3}b + 6{a^2}{b^2} + 4a{b^3} + {b^4}\).
B. \({\left( {a – b} \right)^4} = {a^4} – 4{a^3}b + 6{a^2}{b^2} – 4a{b^3} + {b^4}\).
C. \({\left( {a + b} \right)^4} = {b^4} + 4{b^3}a + 6{b^2}{a^2} + 4b{a^3} + {a^4}\).
D. \({\left( {a + b} \right)^4} = {a^4} + {b^{4.}}\).
Phương pháp
Sử dụng công thức khai triển nhị thức Newton
Giải
Chọn D
\({\left( {a + b} \right)^4} = {a^4} + {b^{4.}}\)
Câu 8: Hệ số của \({x^3}\)trong khai triển biểu thức \({\left( {2x – 1} \right)^4}\) là
A. 32. B. -32. C. 8. D. -8.
Phương pháp
Sử dụng công thức khai triển nhị thức Newton
Giải
Chọn B
\(\begin{array}{l}{\left( {2x – 1} \right)^4} = {\left( {2x} \right)^4} – 4{\left( {2x} \right)^3} + 6{\left( {2x} \right)^2} – 4.2x + 1\\ = 16{x^4} – 32{x^3} + 24{x^2} – 8x + 1\end{array}\)
Vậy hệ số của \({x^3}\) là -32.
Câu 9: Số quy tròn của 314, 87 đến hàng đơn vị là:
A. 315. B. 314,9. C. 310. D. 314.
Phương pháp
Khi quy tròn một số nguyên hoặc một số thập phân đến một hàng nào đó thì số nhận được gọi là số quy tròn của số ban đầu.
– Nếu chữ số ngay sau hàng quy tròn nhỏ hơn 5 thì ta chỉ việc thay thế chữ số đó và các số bên phải nó bởi 0
– Nếu chữ số ngay sau hàng quy tròn lớn hơn hoặc bằng 5 thì ta cũng làm như trên nhưng cộng thêm một đơn vị vào chữ số của hàng quy tròn.
Lời giải
Chọn A
Số quy tròn của 314, 87 đến hàng đơn vị là: 315
Câu 10: Cho mẫu số liệu: 1; 3; 6; 8; 9; 12. Số trung bình cộng của mẫu số liệu là:
A. 6. B. 9. C. 7. D. 6,5.
Phương pháp
Số trung bình cộng \(\overline x \) của mẫu số liệu \({x_1},{x_2},…,{x_n}\) là:
\(\overline x = \frac{{{x_1} + {x_2} + … + {x_n}}}{n}.\)
Lời giải
Chọn D
Số trung bình cộng \(\overline x \) của mẫu số liệu 1; 3; 6; 8; 9; 12 là:
\(\overline x = \frac{{1 + 3 + 6 + 8 + 9 + 12}}{6} = 6,5.\)
Câu 11: Điểm kiểm tra 15 phút môn Toán của 9 bạn tổ 1 như sau:
6 ; 7,3; 8; 6; 7,5; 9; 9; 8,7; 8,5
Tứ phân vị của mẫu số liệu trên là:
A. \({Q_1} = 7,5;{Q_2} = 7,65;{Q_3} = 8,85\).
B. \({Q_1} = 7,65;{Q_2} = 7,5;{Q_3} = 8,85\).
D. \({Q_1} = 6,5;{Q_2} = 8;{Q_3} = 8,85\).
D. \({Q_1} = 8;{Q_2} = 6,65;{Q_3} = 8,85\).
Phương pháp
Sắp thứ tự mẫu số liệu gồm n số liệu thành một dãy không giảm.
Tứ phân vị của mẫu số liệu trên là bộ ba giá trị : Tứ phân vị thứ nhất, Tứ phân vị thứ hai và Tứ phân vị thứ ba; ba giá trị này chia mẫu số liệu thành bốn phần có số lượng phần tử bằng nhau.
– Tứ phân vị thứ hai \({Q_2}\) bằng trung vị.
– Nết n chẵn thì tứ phân vị thứ nhất \({Q_2}\) bằng trung vị của nửa dãy phía dưới, và tứ phân vị thứ ba \({Q_3}\) bằng trung vị của nửa dãy phía trên.
– Nếu n là số lẻ thì tứ phân vị thứ nhất \({Q_2}\) bằng trung vị của nửa dãy phía dưới (không bào gồm \({Q_2}\)) và tứ phân vị thứ ba \({Q_2}\) bằng trung vị của nửa dãy phía trên ( không bao gồm \({Q_2}\))
Giải
Chọn D
Xếp mẫu số liệu theo thứ tự không giảm: 6 6 7,3 7,5 8 8,5 8,7 9 9
– Trung vị của dãy số trên là \({Q_2} = 8\).
– Trung vị của dãy 6 6 7,3 7,5 là \({Q_1} = \frac{{6 + 7,3}}{2} = 6,65\).
– Trung vị của dãy 8,5 8,7 9 9 là \({Q_3} = \frac{{8,7 + 9}}{2} = 8,85\).
Câu 12: Gieo lần lượt hai con súc sắc. Tính xác suất để tổng số chấm trên hai mặt bằng hoặc lớn hơn 8?
A. \(\frac{{11}}{{36}}\)
B.\(\frac{1}{6}\)
C. \(\frac{5}{{18}}\)
D.\(\frac{5}{{12}}\)
Phương pháp
Áp dụng công thức tính xác suất
Giải
Chọn D
\(n\left( \Omega \right) = 36\)
Gọi A là biến cố “ tổng số chấm trên hai mặt bằng hoặc lớn hơn 8”.
\(A = \left\{ {\left\{ {2;6} \right\};\left\{ {3;5} \right\};\left\{ {3;6} \right\};\left\{ {4;4} \right\};\left\{ {4;5} \right\};\left\{ {4;6} \right\};\left\{ {5;3} \right\};\left\{ {5;4} \right\};\left\{ {5;5} \right\};\left\{ {5;6} \right\};\left\{ {6;2} \right\};\left\{ {6;3} \right\};\left\{ {6;4} \right\};\left\{ {6;5} \right\};\left\{ {6;6} \right\}} \right\}\)
\(\begin{array}{l} \Rightarrow n\left( A \right) = 15\\ \Rightarrow P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{15}}{{36}} = \frac{5}{{12}}.\end{array}\)
Câu 13: Gieo một đồng xu hai lần liên tiếp, ta có không gian mẫu là:
A. \(\left\{ {S;N} \right\}\).
B. \(\left\{ {SS;NN} \right\}\).
C. \(\left\{ {SS;SN;NS;NN} \right\}\).
D. \(\left\{ {S;N;SN} \right\}\).
Phương pháp
Áp dụng quy tắc đếm
Giải
Chọn C
Gieo một đồng xu hai lần liên tiếp, ta có không gian mẫu là:
\(\left\{ {SS;SN;NS;NN} \right\}\)
Câu 14: Xác xuất của biến cố A trong trò chơi tung một đồng xu hai lần liên tiếp được tính bằng công thức nào sau đây?
A. \(\frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\).
B. \(\frac{{n\left( \Omega \right)}}{{n\left( A \right)}}\).
C. \(\frac{A}{\Omega }\).
D. \(\frac{\Omega }{A}\).
Phương pháp
Áp dụng công thức tính xác suất
Giải
Chọn A
Xác xuất của biến cố A trong trò chơi tung một đồng xu hai lần liên tiếp được tính bằng công thức :\(\frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\)
Câu 15: Gieo một xúc xắc hai lần liên tiếp. Xác suất của biến cố “ lần thứ nhất xuất hiện mặt 6 chấm” là:
A. \(\frac{1}{2}.\)
B. \(\frac{1}{{36}}.\)
C. \(\frac{1}{6}.\)
D. \(\frac{1}{4}.\)
Phương pháp
Áp dụng công thức tính xác suất
Giải
Chọn C
Gieo một xúc xắc hai lần liên tiếp. Xác suất của biến cố “ lần thứ nhất xuất hiện mặt 6 chấm” là: \(\frac{1}{6}.\)
Câu 16: Xét một phép thử có không gian mẫu và là một biến cố của phép thử đó. Phát biểu nào dưới đây là sai?
A. Xác suất của biến cố A là số \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( P \right)}}.\)
B. \(0 \le P\left( A \right) \le 1.\)
C. \(P\left( A \right) = 0\) khi và chỉ khi là chắc chắn.
D. \(P\left( A \right) = 1 – P\left( {\overline A } \right)\).
Phương pháp
Áp dụng công thức tính xác suất
Giải
Chọn C: \(P\left( A \right) = 0\) khi và chỉ khi là chắc chắn.
Câu 17: Số phần tử không gian mẫu của phép thử gieo đồng thời 1 con xúc xắc và 1 đồng xu là
A. 2. B. 12. C. 8. D. 36.
Phương pháp
Áp dụng quy tăc nhân
Giải
Chọn B
Số phần tử không gian mẫu của phép thử gieo đồng thời 1 con xúc xắc và 1 đồng xu là: 2.6=12
Câu 18: Có 4 viên bi đỏ và 3 viên bi xanh. Lấy ngẫu nhiên 3 viên. Tính xác suất trong 3 viên có 2 viên màu đỏ.
A. \(\frac{6}{{35}}.\)
B. \(\frac{{18}}{{35}}.\)
C. \(\frac{9}{{35}}.\)
D. \(\frac{8}{{35}}.\)
Phương pháp
Áp dụng công thức tính xác suất
Giải
Chọn B
\(n\left( \Omega \right) = C_7^3 = 35\)
Gọi A là biến cố “ có 2 viên màu đỏ”
\(n\left( A \right) = C_4^2.C_3^1 = 18\)
\(p\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{18}}{{35}}.\)
Câu 19: Trong mặt phẳng Oxy, cho vecto \(\vec a = – 3\vec i + \vec j\). Tọa độ của \(\vec a\) là:
A. \(\left( {3;1} \right)\).
B. \(\left( {1;3} \right)\).
C. \(\left( {3; – 1} \right)\).
D. \(\left( { – 3;1.} \right)\)
Phương pháp
Trong mặt phẳng Oxy, tọa độ của \(\vec a\) là: \(\vec a = a\vec i + b\vec j = (a,b)\)
Giải
Chọn D
Trong mặt phẳng Oxy, cho vecto \(\vec a = – 3\vec i + \vec j\). Tọa độ của \(\vec a\) là:\(\left( { – 3;1.} \right)\)
Câu 20: Trong mặt phẳng Oxy, cho hai điểm \(A\left( {2; – 3} \right),B\left( {4;7} \right)\). Tọa độ trung điểm của đoạn thẳng AB là:
A. \(\left( {3;2} \right).\)
B. \(\left( { – 1; – 5} \right).\)
C. \(\left( {1;5} \right)\).
D. \(\left( {2;3} \right).\)
Phương pháp
Tọa độ trung điểm của AB : \(I = \left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\) với \(A({x_A};{y_A});B({x_B};{y_B})\)
Giải
Chọn D
Tọa độ trung điểm của AB: \(I = \left( {\frac{{2 + 4}}{2};\frac{{ – 3 + 7}}{2}} \right) = \left( {3;2} \right)\).
Câu 21: Cho tam giác ABC có \(A\left( {2;6} \right),B\left( { – 2;2} \right),C\left( {8;0} \right)\). Tam giác ABC là:
A. Tam giác đều
B. Tam giác cân tại \(A\)
C. Tam giác vuông tại\(A\)
D. Tam giác vuông cân tại \(A\)
Phương pháp
Với \(A({x_A};{y_A});B({x_B};{y_B})\) thì \(\overrightarrow {AB} = \left( {({x_B} – {x_A});({y_B} – {y_A})} \right) \Rightarrow AB = \sqrt {{{\left( {{x_B} – {x_A}} \right)}^2} + {{\left( {{y_B} – {y_A}} \right)}^2}} \)
Giải
Chọn C
\(\overrightarrow {AB} = \left( { – 4; – 4} \right) \Rightarrow AB = \sqrt {{{\left( { – 4} \right)}^2} + {{\left( { – 4} \right)}^2}} = 4\sqrt 2 \)
\(\overrightarrow {AC} = \left( {6; – 6} \right) \Rightarrow AB = \sqrt {{6^2} + {{\left( { – 6} \right)}^2}} = 6\sqrt 2 \)
\(\overrightarrow {BC} = \left( {10; – 2} \right) \Rightarrow AB = \sqrt {{{10}^2} + {{\left( { – 2} \right)}^2}} = 2\sqrt {26} \)
Ta có \(\overrightarrow {AB} .\overrightarrow {AC} = – 4.6 + \left( { – 4} \right).\left( { – 6} \right) = 0 \Rightarrow AB \bot AC\)
Vậy \(\Delta ABC\) vuông tại \(A.\)
Câu 22: Trong mặt phẳng \(Oxy,\) cho đường thẳng \(d:\,\,3x – 2y + 5 = 0.\) Vectơ nào dưới đây là một vectơ pháp tuyến của \(d\,?\)
A. \(\vec n = \left( {3;\,2} \right).\)
B. \(\vec n = \left( {3;\, – 2} \right).\)
C. \(\vec n = \left( {2;\,3} \right).\)
D. \(\vec n = \left( { – 2;\,3} \right).\)
Phương pháp
Phương trình đường thẳng \(d:ax + by + c = 0\)có VTPT là \(\overrightarrow n = (a;b).\)
Giải
Chọn B
Phương trình đường thẳng \(d:\,\,3x – 2y + 5 = 0.\)có VTPT là \(\vec n = \left( {3;\, – 2} \right).\)
Câu 23: Viết phương trình tham số của đường thẳng đi qua hai điểm và .
A. \(\left\{ \begin{array}{l}x = 1 + 2t\\y = 3 + t\end{array} \right.\)
B.\(\left\{ \begin{array}{l}x = – 1 – 2t\\y = 3 – t\end{array} \right.\)
C. \(\left\{ \begin{array}{l}x = 3 + 2t\\y = – 1 + t\end{array} \right.\)
D. \(\left\{ \begin{array}{l}x = – 1 – 2t\\y = 3 + t\end{array} \right.\)
Phương pháp
Phương trình đường thẳng \(\Delta :\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\end{array} \right.\) có VTCP là \(\overrightarrow u = (a;b).\) đi qua điểm \(A({x_0},{y_0})\)
Giải
Chọn D
\(\overrightarrow {AB} = \left( {4; – 2} \right)\)=> một vtcp của đường thẳng AB là \(\left( { – 2;1} \right)\)
Đường thẳng AB đi qua A và có vtcp \(\left( {2; – 1} \right)\) nên có ptts: .
Câu 24: Xét vị trí tương đối của hai đường thẳng \({d_1}:x – 2y + 1 = 0\)và \({d_2}: – 3x + 6y – 10 = 0\).
A. Song song.
B. Trùng nhau.
C. Vuông góc với nhau.
D. Cắt nhau nhưng không vuông góc nhau.
Phương pháp
Sử dụng công thức vị trí tương đối của hai đường thẳng.
Giải
Chọn A
Hai đường thẳng trên có vtpt lần lượt là \({\vec n_1}\left( {1; – 2} \right),{\vec n_2}\left( { – 3;6} \right)\)
Ta có \({\vec n_2} = – 3{\vec n_1}\) và \(1 \ne – 10\) nên hai đường thẳng đã cho song song với nhau.
Câu 25: Cho đường thẳng và . Tính cosin của góc tạo bởi hai đường thẳng đã cho.
A. \(\frac{{3\sqrt {10} }}{{10}}\)
B. \(\frac{3}{5}\)
C. \(\frac{{\sqrt {10} }}{{10}}\)
D. \(\frac{3}{{10}}\)
Phương pháp
Áp dụng công thức tính góc giữa hai đường thẳng có: \(\cos \left( {{d_1},{d_2}} \right) = \frac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}}\).
Giải
Chọn A
\(\begin{array}{l}\overrightarrow {{n_1}} \left( {10;5} \right)\\\overrightarrow {{u_2}} \left( {1; – 1} \right) \Rightarrow \overrightarrow {{n_2}} \left( {1;1} \right)\end{array}\)
\(\cos \left( {{d_1},{d_2}} \right) = \frac{{\left| {10.1 + 5.1} \right|}}{{\sqrt {{{10}^2} + {5^2}} \sqrt {{1^2} + {1^2}} }} = \frac{{3\sqrt {10} }}{{10}}\).
Câu 26: Tọa độ tâm I và bán kính R của đường tròn \( (C):{(x – 1)^2} + {(y + 3)^2} = 16 \)là:
A. I( – 1;3),R = 4
B. I(1; -3),R = 4
C. I(1; -3),R = 16
D. I(- 1;3),R = 16
Phương pháp
Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là : \( {(x – a)^2} + {(y – b)^2} = {R^2} \)
Giải
Chọn B
Tọa độ tâm I và bán kính R của đường tròn\( (C):{(x – 1)^2} + {(y + 3)^2} = 16 \) là:\( I(1; – 3),R = 4 \)
Câu 27: Đường tròn có tâm và bán kính lần lượt là:
A. \(I(3; – 1),R = 4\)
B.\(I( – 3;1),R = 4\)
C. \(I(3; – 1),R = 2\)
D. \(I( – 3;1),R = 2\)
Phương pháp
Phương trình đường tròn có dạng \({x^2} + {y^2} – 2ax – 2by + c = 0\,\,\left( {{a^2} + {b^2} – c > 0} \right)\). và tọa độ tâm \(I(a,b)\), bán kính \(\,R = \sqrt {{a^2} + {b^2} – c} \)
Giải
Chọn C
\(I\left( {\frac{{ – 6}}{{ – 2}};\frac{2}{{ – 2}}} \right) = \left( {3; – 1} \right);\,R = \sqrt {{3^2} + {1^2} – 6} = 2\).
Câu 28: Đường tròn đường kính với có phương trình là:
A. \({\left( {x – 2} \right)^2} + {(y – 3)^2} = 5\)
B. \({\left( {x + 1} \right)^2} + {(y + 2)^2} = 17\)
C. \({\left( {x – 2} \right)^2} + {(y + 3)^2} = \sqrt 5 \)
D. \({\left( {x – 2} \right)^2} + {(y + 3)^2} = 5\)
Phương pháp
Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là : \({(x – a)^2} + {(y – b)^2} = {R^2}\)
Giải
Chọn D
Tâm I của đường tròn chính là trung điểm của AB
\(\begin{array}{l}I\left( {\frac{{3 + 1}}{2};\frac{{ – 1 – 5}}{2}} \right) = \left( {2; – 3} \right)\\AB = \sqrt {{{\left( {3 – 1} \right)}^2} + {{\left( { – 1 + 5} \right)}^2}} = 2\sqrt 5 \Rightarrow R = \frac{{AB}}{2} = \sqrt 5 \end{array}\)
Phương trình đường tròn:
Câu 29: Elip có độ dài trục lớn là 10 và có một tiêu điểm . Phương trình chính tắc của elip là:
A. \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\)
B. \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{16}} = 1\)
C. \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{81}} = 1\)
D. \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\)
Phương pháp
Phương trình Elip \(\left( E \right):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
Giải
Chọn D
Độ dài trục lớn 2a=10 => a = 5.
\(c = 3 \Rightarrow {b^2} = {a^2} – {c^2} = {5^2} – {3^2} = 16\)
Phương trình chính tắc của elip:
Câu 30: Hyperbol trong hệ trục tọa độ Oxy nào dưới đây có phương trình chính tắc dạng \(\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} = 1\left( {a > 0,b > 0} \right)\)?
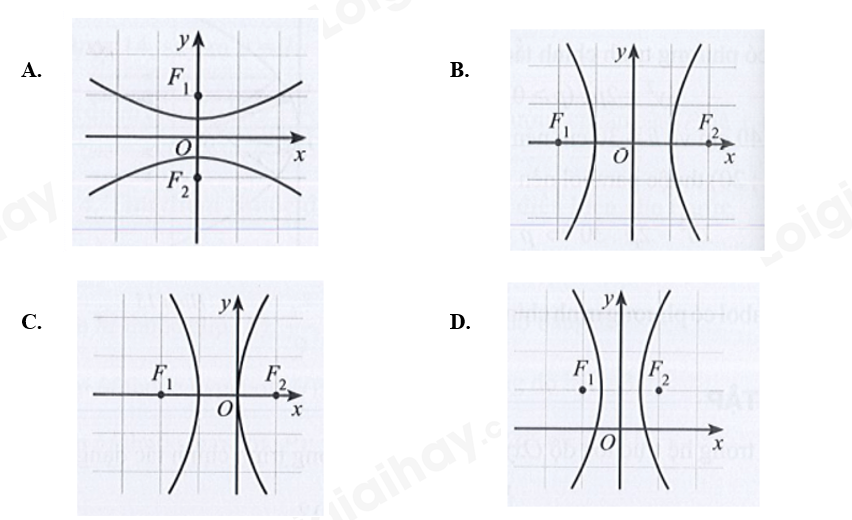
Phương pháp
Dựa vào dáng điệu của hypebol \(\left( H \right):\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} = 1\)
Giải
Chọn B.
Hai tiêu điểm thuộc trục hoành và nhận O làm trung điểm.
Câu 31: Parabol (P) có phương trình đường chuẩn là \(x + \frac{1}{4} = 0\). Phương trình chính tắc của (P) là:
A. \({y^2} = \frac{1}{2}x.\)
B. \({y^2} = 2x\).
C. \({y^2} = x.\)
D. \({y^2} = 4x.\)
Phương pháp
Phương trình parabol: \({y^2} = 2px\).
Giải
Chọn C.
Phương trình đường chuẩn là \(x + \frac{1}{4} = 0 \Rightarrow p = \frac{1}{2}\).
Phương trình parabol: \({y^2} = 2px = 2.\frac{1}{2}x = x\).
Câu 32: Hệ số lớn nhất trong khai triển biểu thức \({\left( {x + 1} \right)^5}\)là:
A. 10. B. 5. C. 6. D. 4.
Phương pháp
Sử dụng công thức khai triển nhị thức Newton
Lời giải
Chọn A
Trong khai triển nhị thức Niu-tơn của \({\left( {x + 1} \right)^5} = {x^5} + 5{x^4} + 10{x^3} + 10{x^2} + 5x + 1\) có \(4 + 1 = 5\)
Vậy hệ số lớn nhất trong khai triển biểu thức \({\left( {x + 1} \right)^5}\)là: 10
Biểu đồ ở hình 1 biểu diễn nhiệt độ không khí tại Hà Nội giai đoạn 2014 – 2019. Sử dụng mẫu số liệu từ biểu đồ này để hoàn thành các câu 34, 34, 35.
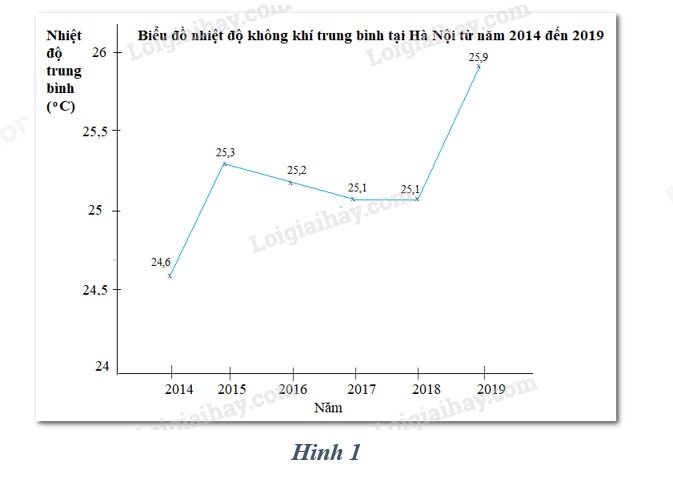
Câu 33: Khoảng biến thiên của mẫu số liệu là:
A. 1. B. 1,3. C. 50,5. D. 0,65.
Phương pháp
Trong một mẫu số liệu, khoảng biến thiên là hiệu số giữa giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đó.
Ta có thể tính khoảng bến thiên R của mẫu số liệu theo công thức \(R = {x_{\max }} – {x_{\min }}\), trong đó \({x_{\max }}\) là giá trị lớn nhất, \({x_{\min }}\)là giá trị nhỏ nhất của mẫu số liệu đó.
Giải
Chọn B.
Khoảng biến thiên: 25,9 -24,6 = 1,3.
Câu 34: Khoảng tứ phân vị của mẫu số liệu là:
A. 0,2. B. 0,15. C. 25,15. D. 0,05.
Phương pháp
Giả sử \({Q_1},{Q_2},{Q_3}\) là tứ phân vị của mẫu số liệu.
Sắp thứ tự mẫu số liệu gồm n số liệu thành một dãy không giảm.
Tứ phân vị của mẫu số liệu trên là bộ ba giá trị : Tứ phân vị thứ nhất, Tứ phân vị thứ hai và Tứ phân vị thứ ba; ba giá trị này chia mẫu số liệu thành bốn phần có số lượng phần tử bằng nhau.
– Tứ phân vị thứ hai \({Q_2}\) bằng trung vị.
– Nết n chẵn thì tứ phân vị thứ nhất \({Q_2}\) bằng trung vị của nửa dãy phía dưới, và tứ phân vị thứ ba \({Q_3}\) bằng trung vị của nửa dãy phía trên.
– Nếu n là số lẻ thì tứ phân vị thứ nhất \({Q_2}\) bằng trung vị của nửa dãy phía dưới (không bào gồm \({Q_2}\)) và tứ phân vị thứ ba \({Q_2}\) bằng trung vị của nửa dãy phía trên ( không bao gồm \({Q_2}\))
Ta gọi hiệu \({\Delta _Q} = {Q_3} – {Q_1}\) là khoảng tứ phân vị của mẫu số liệu đó.
Giải
Chọn A.
Xếp dãy số liệu theo thứ tự không giảm: 24,6 25,1 25,1 25,2 25,3 25,9
\({Q_2} = \frac{{25,1 + 25,2}}{2} = 25,15;{Q_1} = 25,1;{Q_3} = 25,3\)
Khoảng tứ phân vị \({Q_3} – {Q_1} = 0,2\).
Câu 35: Phương sai của mẫu số liệu gần nhất với số nào sau đây:
A. 0,1. B. 0,15. C. 0,147. D. 1.
Phương pháp
Cho mẫu số liêu thống kê có n giá trị \({x_1},{x_2},…,{x_n}\) và số trung bình cộng \(\overline x \).
Ta gọi số \({s^2} = \frac{{{{({x_1} – \overline x )}^2} + {{({x_2} – \overline x )}^2} + … + {{({x_n} – \overline x )}^2}}}{n}\) là phương sai của mẫu số liệu
Giải
Chọn C.
Trung bình cộng \(\overline X = \frac{{24,6 + 25,1.2 + 25,2 + 25,3 + 25,9}}{6} = 25,2\)
Phương sai: \(\begin{array}{l}\frac{{{{\left( {24,6 – 25,2} \right)}^2} + {{\left( {25,1 – 25,2} \right)}^2}.2 + {{\left( {25,2 – 25,2} \right)}^2} + {{\left( {25,3 – 25,2} \right)}^2} + {{\left( {25,9 – 25,2} \right)}^2}}}{6}\\ = 0,14666667\end{array}\)
PHẦN II: TỰ LUẬN
Câu 36: a) (1.0 điểm) Giả sử hệ số của x trong khai triển biểu thức \({\left( {ax + \frac{1}{x}} \right)^5}\) bằng 270. Tìm giá trị của a.
b) (0.5 điểm) Tìm số đường chéo của 1 đa giác lồi có 10 cạnh.
Phương pháp
a) Sử dụng khai triển nhị thức Newton
b) Sử dụng công thức tổ hợp
Giải
a) \(\begin{array}{l}{\left( {ax + \frac{1}{x}} \right)^5} = {\left( {ax} \right)^5} + 5{\left( {ax} \right)^4}.\frac{1}{x} + 10{\left( {ax} \right)^3}.\frac{1}{{{x^2}}} + 10{\left( {ax} \right)^2}.\frac{1}{{{x^3}}} + 5ax.\frac{1}{{{x^4}}} + \frac{1}{{{x^5}}}\\ = {a^5}{x^5} + 5{a^4}{x^3} + 10{a^3}x + \frac{{10{a^2}}}{x} + \frac{{5a}}{{{x^3}}} + \frac{1}{{{x^5}}}\end{array}\)
Theo đề ta có \(10{a^3} = 270 \Rightarrow {a^3} = 27 \Rightarrow a = 3\).
b) Cứ hai đỉnh của đa giác tạo thành 1 cạnh hoặc 1 đường chéo.
Tổng số đường chéo và cạnh: \(C_{10}^2\)
Số đường chéo: \(C_{10}^2\)-10=35.
Câu 37: a) (1.0 điểm ) Cho tam giác ABC có phương trình các đường thẳng \(AB:2x – 3y – 1 = 0;\)
\(BC:x + 3y + 7 = 0;\) \(CA:5x – 2y + 1 = 0\). Viết phương trình tổng quát của đường cao kẻ từ \(B\)
b) (0.5 điểm) Cho tam giác ABC với \(A\left( { – 1;0} \right),B\left( {2;3} \right),C\left( {3; – 6} \right)\) và đường thẳng \(d:x – 2y – 3 = 0\). Tìm điểm M trên d sao cho \(\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right|\) nhỏ nhất.
Phương pháp
Phương trình đường thẳng \(d:ax + by + c = 0\)có VTPT là \(\overrightarrow n = (a;b).\)
Giải
a) Đỉnh B là giao điểm của hai đường thẳng AB và BC nên tọa độ đỉnh B là nghiệm của hpt \(\left\{ \begin{array}{l}2x – 3y = 1\\x + 3y = – 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = – 2\\y = \frac{{ – 5}}{3}\end{array} \right.\) =>\(B\left( { – 2; – \frac{3}{5}} \right)\).
Gọi d là đường cao kẻ từ \(B.\) Vì d vuông góc với AC nên d có dạng \(2x + 5y + c = 0\).
Mà \(B \in d \Leftrightarrow 2\left( { – 2} \right) + 5\left( {\frac{{ – 3}}{5}} \right) + c = 0 \Leftrightarrow c = 7\).
Vậy d: \(2x + 5y + 7 = 0.\)
b) Gọi \(M\left( {2y + 3;y} \right)\)
\(\begin{array}{l}\overrightarrow {MA} = \left( { – 4 – 2y; – y} \right),\overrightarrow {MB} = \left( { – 1 – 2y;3 – y} \right),\overrightarrow {MC} = \left( { – 2y; – 6 – y} \right)\\ \Rightarrow \overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = \left( {4 – 3x; – 3 – 3y} \right)\\ \Rightarrow \left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right| = \sqrt {{{\left( { – 5 – 6y} \right)}^2} + \left( { – 3 – 3y} \right)} = \sqrt {45{y^2} + 78y + 34} \end{array}\)
Xét parabol \(\left( P \right):y = 45{x^2} + 78x + 34\) có hệ số a = 45 >0 và đỉnh \(I\left( {\frac{{ – 78}}{{90}};\frac{{ – 13}}{{15}}} \right)\)
Do đó, \(\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right|\) nhỏ nhất đạt GTNN là \(\frac{{ – 13}}{{15}}\) khi \(y = \frac{{ – 78}}{{90}}\).
Vậy \(M\left( {\frac{{19}}{{15}};\frac{{ – 78}}{{90}}} \right)\).