Giải Đề bài Đề thi giữa kì 1 – Đề số 4 – Đề thi đề kiểm tra Toán lớp 10 Cánh diều.
Câu hỏi/Đề bài:
I. PHẦN TRẮC NGHIỆM
Câu 1. Kí hiệu nào sau đây viết đúng mệnh đề: “\(\sqrt 2 \) là số hữu tỉ”
A. \(\sqrt 2 = \mathbb{Q}\) B. \(\sqrt 2 \in \mathbb{Q}\) C. \(\sqrt 2 \subset \mathbb{Q}\) D. \(\sqrt 2 \notin \mathbb{Q}\)
Câu 2. Mệnh đề phủ định của mệnh đề \(\forall x \in \mathbb{R},{x^2} – x – 2 > 0\) là:
A. \(\forall x \in \mathbb{R},{x^2} – x – 2 < 0\). B. \(\exists x \in \mathbb{R},{x^2} – x – 2 < 0\). C. \(\forall x \in \mathbb{R},{x^2} – x – 2 \le 0\). D. \(\exists x \in \mathbb{R},{x^2} – x – 2 \le 0\)
Câu 3. Cho \(A = \{ 1;2;3;4;a;b\} \). Xét các mệnh đề :
\((I):1 \in A\) \((II):\{ 3;4\} \in A\) \((III):\{ 2;a;b\} \subset A\) \((IV):\{ 0;b\} \subset A\)
Số mệnh đề đúng là
A. \(0\) B. \(1\). C. \(2\). D. \(3\).
Câu 4. Cho \(A = ( – 2;5]\) và \(B = (m; + \infty )\). Tìm \(m \in \mathbb{Z}\) để \(A \cap B\) chứa đúng 5 số nguyên là:
A. \( – 1\). B. \(0\). C. \(1\) D. \(2\)
Câu 5. Mỗi học sinh của lớp 10E đều học giỏi môn Sử hoặc Địa, biết rằng có 28 học sinh giỏi Sử, 33 học sinh giỏi Địa và 15 em học giỏi cả hai môn. Hỏi lớp 10E có tất cả bao nhiêu học sinh ?
A. \(42\). B. \(45\). C. \(46\). D. \(47\).
Câu 6. Miền nghiệm của bất phương trình \(2x + 3y \ge 12\) là:
A. 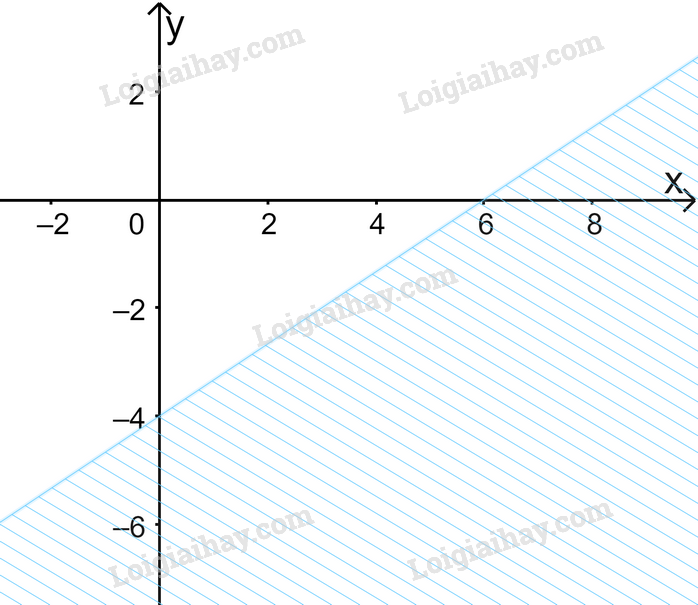 B.
B. 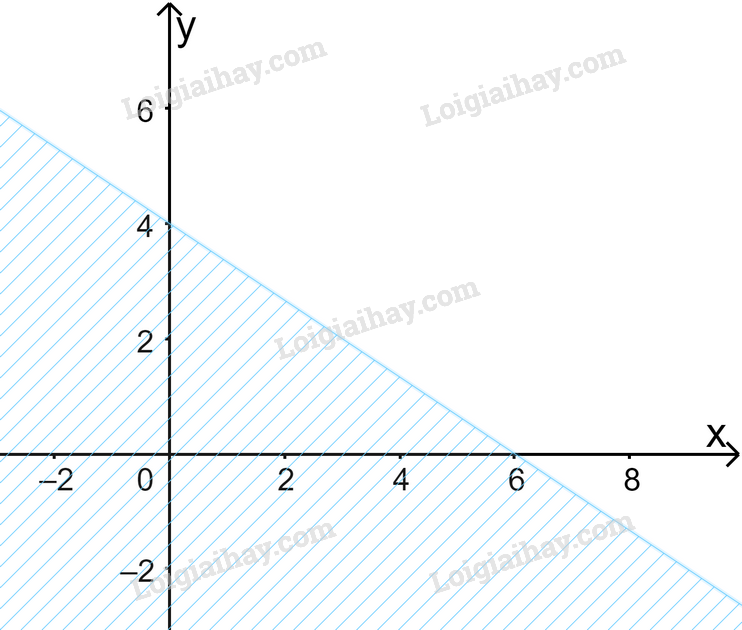
C. 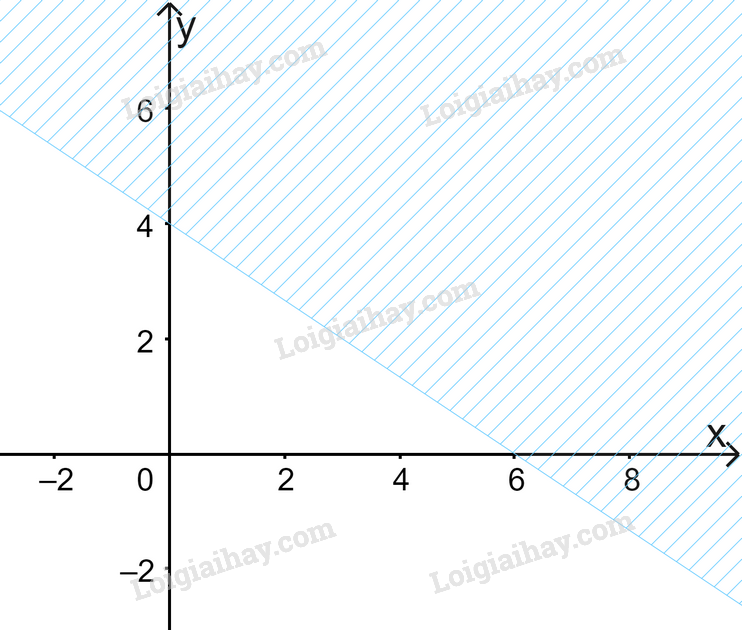 D.
D. 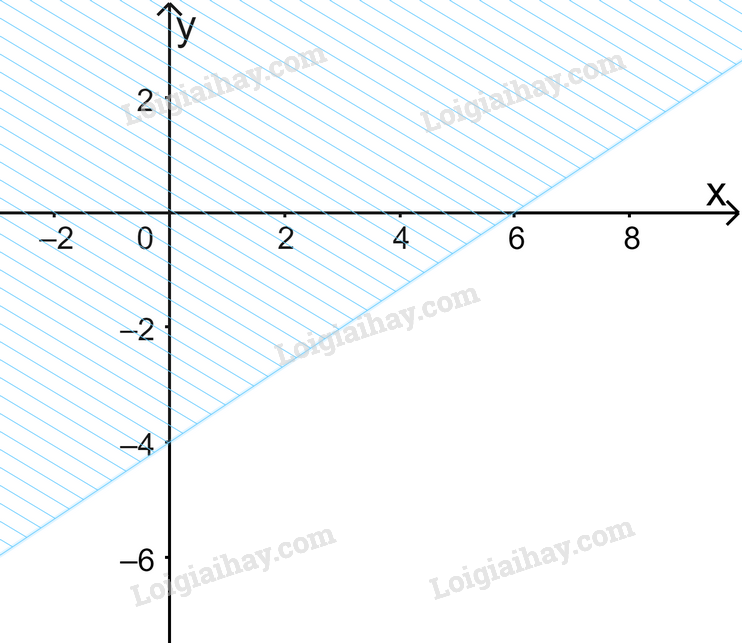
Câu 7. Giá trị lớn nhất của \(F(x;y) = 3x + 4y\), với điều kiện \(\left\{ \begin{array}{l}x \ge 0\\0 \le y \le 5\\x + y – 2 \ge 0\\3x – y \le 6\end{array} \right.\)
A.\(6\) B. \(8\) C.\(20\) D. \(33\)
Câu 8. Tập xác định của hàm số \(y = \frac{{x + 2}}{{\sqrt {{x^2} – 9} }}\)
A. \(\mathbb{R}\). B. \(\mathbb{R}{\rm{\backslash }}\{ 3\} \) C. \(\mathbb{R}{\rm{\backslash }}\{ – 3;3\} \). D. \(\mathbb{R}{\rm{\backslash }}[ – 3;3]\).
Câu 9. Parabol \((P):y = {x^2} – 3x + 5\) có tổng số điểm chung với hai trục là
A.\(0\) B. \(1\). C. \(2\). D. \(3\).
Câu 10. Cho hàm số \(f(x)\) xác định trên \(\mathbb{R}\) và có bảng biến thiên như sau:
Khẳng định nào sau đây đúng?
A. \(f( – 5) < f( – 3)\) B. \(f(0) < f(2)\) C. \(f(0) > f(1)\) D. \(f(22) > f(20)\)
Câu 11. Đường thẳng nào dưới đây vuông góc với đường thẳng \(y = \sqrt 7 x + 3\)
A. \(y = – \sqrt 7 x + 1\) B. \(y = \frac{{\sqrt 7 }}{7}x – 3\) C. \(y = \sqrt 7 x + 5\). D. \(y = – \frac{{\sqrt 7 }}{7}x\).
Câu 12. Cho hàm số \(f(x) = {x^2} – 2x + 3\). Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên \(( – \infty ;1)\), nghịch biến trên \((1; + \infty )\).
B. Hàm số đồng biến trên \((1; + \infty )\), nghịch biến trên \(( – \infty ;1)\).
C. Hàm số nghịch biến trên \(\mathbb{R}\).
D. Hàm số đồng biến trên \(\mathbb{R}\).
Câu 13. Điểm \(A( – 2;3)\) thuộc miền nghiệm của hệ bất phương trình nào dưới đây?
A. \(\left\{ \begin{array}{l}x + 2y > 9\\3x – y < 5\end{array} \right.\) B. \(\left\{ \begin{array}{l}2x – y > 7\\x + y \le 3\end{array} \right.\) C. \(\left\{ \begin{array}{l}3x + 5 \le 10\\4x – y > 3\end{array} \right.\) D. \(\left\{ \begin{array}{l}2x + 5y > 8\\x – 3y \le 4\end{array} \right.\)
Câu 14. Cho hàm số \(f(x) = \left\{ \begin{array}{l}\sqrt {x – 1} + 2\quad (x \ge 1)\\3{x^2} – x + 1\quad (x < 1)\end{array} \right.\). Giá trị của \(2.f( – 3) – 4.f(1)\) là:
A. \(50\) B. \(54\) C. \( – 8\). D. \( – 4\).
Câu 15. Cho bất phương trình \(5(2x + 3y) – 4(2x + y – 7) > x – 3y\). Điểm nào dưới đây không thuộc miền nghiệm của hệ đã cho?
A. \(O(0;0)\) B. \(A(1;0)\). C. \(B(3;2)\). D. \(C(0; – 2)\)
II. PHẦN TỰ LUẬN
Câu 1. Tìm \(A \cap B,A \cup B,A{\rm{\backslash }}B,B{\rm{\backslash }}A\), biết:
a) \(A = \{ 0;1;2;3\} ,B = \{ x \in \mathbb{Z}|{x^2} – 2x – 3 = 0\} \)
b) \(A = ( – 1;5),B = (3; + \infty )\)
c) \(A = [1,4),B = [4; + \infty )\)
d) \(A = \{ x \in \mathbb{R}|1 \le x < 6\} ,B = (2;9)\)
Câu 2. Một công ty kinh doanh thương mại chuẩn bị cho một đợt khuyến mại nhằm thu hút khách hàng bằn cách tiến hành quảng cáo sản phẩm của công ty trên hệ thống phát thanh và truyền hình. Chi phí cho 1 phút quảng cáo trên sóng phát thanh là 800.000 đồn, trên sóng truyền hình là 4.000.000 đồng. Đài phát thanh chỉ nhận phát các chương trình quảng cáo dài ít nhất là 5 phút. Do nhu cầu quảng cáo trên truyền hình lớn nên đài truyền hình chỉ nhận phát các chươn trình tối đa là 4 phút. Theo các phân tích, cùng thời lượng một phút quảng cáo, trên truyền hình sẽ có hiệu quả gấp 6 lần trên sóng phát thanh. Công ty dự định chi tối đa 16.000.000 dùng cho quảng cáo. Công ty đặt thời lượng quảng cáo trên sóng phát thanh và truyền hình như thế nào để hiệu quả nhất?
Câu 3.
a) Xác định parabol (P) biết \((P):y = a{x^2} + bx + c\) đi qua A(4;3) và có đỉnh \(I(2; – 1)\)
b) Xét sự biến thiên và vẽ đồ thị hàm số trên.
Câu 4. Tìm giá trị lớn nhất, nhỏ nhất (nếu có) của hàm số: \(y = 3{x^2} – 6x + 7\) trên đoạn [-2;5].