Hướng dẫn giải Lời giải chi tiết Đề thi giữa kì 1 – Đề số 4 – Đề thi đề kiểm tra Toán lớp 10 Cánh diều.
Câu hỏi/Đề bài:
I. PHẦN TRẮC NGHIỆM
|
1. B |
2. D |
3. C |
4. B |
5. C |
|
6. B |
7. D |
8. D |
9. B |
10. B |
|
11. D |
12. B |
13. D |
14. B |
15. C |
Câu 1
Cách giải:
Tập hợp các số hữu tỉ: \(\mathbb{Q}\)
“\(\sqrt 2 \) là số hữu tỉ” viết là: \(\sqrt 2 \in \mathbb{Q}\)
Chọn B.
Câu 2:
Cách giải:
Phủ định của mệnh đề \(\forall x \in \mathbb{R},{x^2} – x – 2 > 0\) là \(\exists x \in \mathbb{R},{x^2} – x – 2 \le 0\)
Chọn D.
Câu 3:
Cách giải:
\((I):1 \in A\) đúng
\((II):\{ 3;4\} \in A\) sai. Vì kí hiệu \( \in \) không dùng trong quan hệ giữa 2 tập hợp.
\((III):\{ 2;a;b\} \subset A\) đúng.
\((IV):\{ 0;b\} \subset A\) sai vì \(0 \notin A\).
Vậy có 2 mệnh đề đúng.
Chọn C.
Câu 4:
Cách giải:
+ Nếu \(m \ge 5\) thì \(A \cap B = \emptyset \)
+ Nếu \(m \le – 2\) thì \(( – 2;5] \subset (m; + \infty ) \Rightarrow A \cap B = ( – 2;5]\), chứa 7 số nguyên
là -1 ; 0 ;1 ;2 ;3 ;4 ;5 (nhiều hơn 5) nên ta loại trường hợp \(m \le – 2\)
+ Nếu \( – 2 < m < 5\) thì \(A \cap B = ( – 2;5] \cap (m; + \infty ) = (m;5]\).
Để \(A \cap B\) chứa đúng 5 số nguyên thì \((m;5]\) chứa đúng 5 số nguyên là : 5 ;4 ;3 ;2 ;1
Hay \(m = 0\)
Chọn B.
Câu 5
Cách giải:
Gọi X là tập hợp học sinh lớp 10E
A là tập hợp các học sinh học giỏi môn Sử.
B là là tập hợp các học sinh học giỏi môn Địa.
Suy ra :
\(A \cap B\) là tập hợp các học sinh học giỏi cả hai môn Sử và Địa.
\(A \cup B\) là tập hợp các học sinh lớp 10E
Ta có : \(n(A) = 28;n(B) = 33;n\left( {A \cap B} \right) = 15\)
\( \Rightarrow \) Số học sinh lớp 10E là:
\(n\left( {A \cup B} \right) = n(A) + n(B) – n\left( {A \cap B} \right) = 28 + 33 – 15 = 46\) (học sinh)
Chọn C.
Câu 6
Hướng dẫn:
Xác định đường thẳng \(2x + 3y = 12\) và xét một điểm (không thuộc đường thẳng) xem có thuộc miền nghiệm hay không.
Cách giải:
Đường thẳng \(2x + 3y = 12\) đi qua điểm có tọa độ (6;0) và (0;4) => Loại A, D.
Xét điểm O(0;0), ta có: \(2.0 + 3.0 = 0 < 12\) nên O không thuộc miền nghiệm của BPT đã cho.
Chọn B.
Câu 7:
Hướng dẫn:
Bước 1: Biểu diễn miền nghiệm, xác định các đỉnh của miền nghiệm
Bước 2: Thay tọa độ các đỉnh vào \(F(x;y) = 3x + 4y\), kết luận giá trị nhỏ nhất.
Cách giải:
Xét hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\0 \le y \le 5\\x + y – 2 \ge 0\\3x – y \le 6\end{array} \right.\)
Biểu diễn miền nghiệm của hệ, ta được
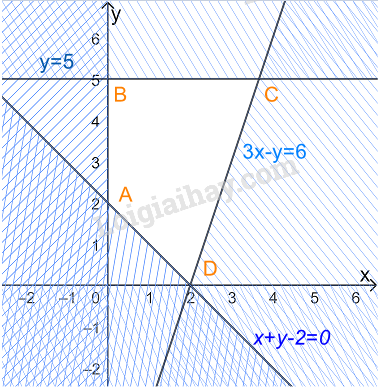
Miền nghiệm là miền tứ giác ABCD trong đó \(A\left( {0;2} \right),{\rm{ }}B\left( {0;5} \right),{\rm{ }}C\left( {\frac{{11}}{3};5} \right),D(2;0)\)
Thay tọa độ các điểm A, B, C, D vào \(F(x;y) = 3x + 4y\) ta được
\(F(0;2) = 3.0 + 4.2 = 8\)
\(F(0;5) = 3.0 + 4.5 = 20\)
\(F\left( {\frac{{11}}{3};5} \right) = 3.\frac{{11}}{3} + 4.5 = 33\)
\(F(2;0) = 3.2 + 4.0 = 6\)
Vậy giá trị lớn nhất của F bằng 33.
Chọn D.
Câu 8:
Hướng dẫn:
\(\frac{{f(x)}}{{\sqrt {g(x)} }}\) xác định khi \(\left\{ \begin{array}{l}g(x) \ne 0\\g(x) \ge 0\end{array} \right.\) hay \(g(x) > 0\).
Cách giải:
Hàm số \(y = \frac{{x + 2}}{{\sqrt {{x^2} – 9} }}\) xác định khi \(\left\{ \begin{array}{l}{x^2} – 9 \ne 0\\{x^2} – 9 \ge 0\end{array} \right.\) hay \({x^2} – 9 > 0\).
\( \Leftrightarrow {x^2} > 9 \Leftrightarrow |x|\; > 3 \Leftrightarrow \left[ \begin{array}{l}x > 3\\x < – 3\end{array} \right.\)
Tập xác định là \(( – \infty ; – 3) \cup (3; + \infty )\) hay \(\mathbb{R}{\rm{\backslash }}[ – 3;3]\)
Chọn D.
Câu 9:
Hướng dẫn:
Số giao điểm của Parabol \((P):y = f(x)\) với trục hoành là số nghiệm của phương trình \(f(x) = 0\).
Cách giải:
Xét phương trình hoành độ giao điểm của (P) với trục hoành là:
\({x^2} – 3x + 5 = 0\) (*)
Mà \({x^2} – 3x + 5 = {\left( {x – \frac{3}{2}} \right)^2} + \frac{{11}}{4} \ge \frac{{11}}{4} > 0\)
Do đó phương trình (*) vô nghiệm hay parabol không cắt trục hoành.
(P) cắt trục tung tại A(0;5), do đó tổng số điểm chung của (P) với hai trục là 1.
Chọn B.
Câu 10:
Cách giải:
Từ bảng biến thiên ta suy ra
Hàm số đồng biến trên \(( – 1;3)\)
Hàm số nghịch biến trên \(( – \infty ; – 1)\) và \((3; + \infty )\)
+ Vì \( – 5, – 3 \in ( – \infty ;1)\) và \( – 5 f( – 3)\) => A sai.
+ Vì \(0,2 \in ( – 1;3)\) và \(0 < 2\) nên \(f(0) B đúng.
+ Vì \(0,1 \in ( – 1;3)\) và \(0 < 1\) nên \(f(0) C sai.
+ Vì \(20,22 \in (3; + \infty )\) và \(20 f(22)\) => D sai.
Chọn B.
Câu 11
Hướng dẫn:
Đường thẳng vuông góc với đường thẳng \(y = ax + b\) có dạng \(y = a’x + b’\) với \(a.a’ = – 1\)
Cách giải:
Đường thẳng d: \(y = \sqrt 7 x + 3\) có hệ số góc \(k = \sqrt 7 \)
Đường thẳng d’ vuông góc với d có hệ số góc \(k’ = \frac{{ – 1}}{{\sqrt 7 }} = – \frac{{\sqrt 7 }}{7}\)
Đường thẳng d’ có dạng \(y = – \frac{{\sqrt 7 }}{7}x + b’\)
Chọn D.
Câu 12:
Cách giải:
Xét hàm số \(f(x) = {x^2} – 2x + 3\), có \(a = 1 > 0,b = – 2\)
\( \Rightarrow \frac{{ – b}}{{2a}} = 1;f(1) = 2\)
Bảng biến thiên:
Hàm số đồng biến trên \((1; + \infty )\) và nghịch biến trên \(( – \infty ;1)\).
Chọn B.
Câu 13.
Hướng dẫn:
Thay tọa độ điểm A vào hệ BPT, hệ nào cho ta các mệnh đề đúng thì điểm A thuộc miền nghiệm của hệ BPT đó.
Cách giải
+ Xét hệ \(\left\{ \begin{array}{l}x + 2y > 9\\3x – y 9\) sai nên A(-2;3) không thuộc miền nghiệm của hệ BPT.
+ Xét hệ \(\left\{ \begin{array}{l}2x – y > 7\\x + y \le 3\end{array} \right.\), thay \(x = – 2,y = 3\) ta được: \( – 2.2 – 3 = – 7 > 7\) sai nên A(-2;3) không thuộc miền nghiệm của hệ BPT.
+ Xét hệ \(\left\{ \begin{array}{l}3x + 5 \le 10\\4x – y > 3\end{array} \right.\), thay \(x = – 2,y = 3\) ta được: \(3.( – 2) + 5 = – 1 \le 10\) sai nên A(-2;3) không thuộc miền nghiệm của hệ BPT.
+ Xét hệ \(\left\{ \begin{array}{l}2x + 5y > 8\\x – 3y \le 4\end{array} \right.\), thay \(x = – 2,y = 3\) ta được: \(\left\{ \begin{array}{l}2.( – 2) + 5.3 = 11 > 8\\ – 2 – 3.3 = – 9 \le 4\end{array} \right.\) đúng nên A(-2;3) thuộc miền nghiệm của hệ BPT.
Chọn D.
Câu 14:
Cách giải:
Tại \(x = – 3 < 1\) thì \(f( – 3) = 3.{( – 3)^2} – ( – 3) + 1 = 31\)
Tại \(x = 1 \ge 1\) thì \(f(0) = \sqrt {1 – 1} + 2 = 2\)
\( \Rightarrow 2.f( – 3) – 4.f(0) = 2.31 – 4.2 = 54\)
Chọn B.
Câu 15. Cho bất phương trình \(5(2x + 3y) – 4(2x + y – 7) > x – 3y\). Điểm nào dưới đây thuộc miền nghiệm của hệ đã cho?
A. \(O(0;0)\) B. \(A(1;0)\). C. \(B(3; – 2)\). D. \(C(0;2)\)
Cách giải:
Ta có: \(5(2x + 3y) – 4(2x + y – 7) > x – 3y\)
\(\begin{array}{l} \Leftrightarrow 10x – 15y – 8x – 4y + 28 – x + 3y > 0\\ \Leftrightarrow x – 16y + 28 > 0\end{array}\)
Thay tọa độ các điểm vào BPT:
+ Vì \(0 – 16.0 + 28 = 28 > 0\) nên \(O(0;0)\) thuộc miền nghiệm
+ Vì \(1 – 16.0 + 28 = 29 > 0\) nên \(A(1;0)\) thuộc miền nghiệm
+ Vì \(3 – 16.2 + 28 = – 1 < 0\) nên \(B(3;2)\) không thuộc miền nghiệm
+ Vì \(0 – 16.( – 2) + 28 = 60 > 0\) nên \(C(0; – 2)\) thuộc miền nghiệm
Chọn C
II. PHẦN TỰ LUẬN
Câu 1
Hướng dẫn:
a) \(A \cap B = \{ x \in A|x \in B\} \)
b) \(A \cup B = \{ x|x \in A\) hoặc \(x \in B\} \)
c, d) \(A{\rm{\backslash }}B = \{ x \in A|x \notin B\} \)
Cách giải:
a) \(A = \{ 0;1;2;3\} ,B = \{ x \in \mathbb{Z}|{x^2} – 2x – 3 = 0\} \)
Ta có: \({x^2} – 2x – 3 = 0 \Leftrightarrow \left\{ \begin{array}{l}x = 3\\x = – 1\end{array} \right.\)
\( \Rightarrow B = \{ x \in \mathbb{Z}|{x^2} – 2x – 3 = 0\} = \{ – 1;3\} \)
\(A \cap B = \{ 3\} ,A \cup B = \{ – 1;0;1;2;3\} ,A{\rm{\backslash }}B = \{ 0;1;2\} ,B{\rm{\backslash }}A = \{ – 1\} \)
b) \(A = ( – 1;5),B = (3; + \infty )\)
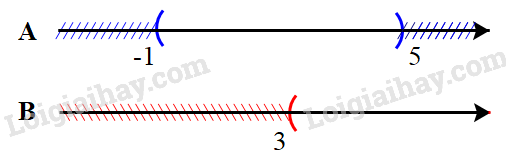
\(A \cap B = (3;5),A \cup B = ( – 1; + \infty ),A{\rm{\backslash }}B = ( – 1;3],B{\rm{\backslash }}A = [5; + \infty )\)
c) \(A = [1,4),B = [4; + \infty )\)
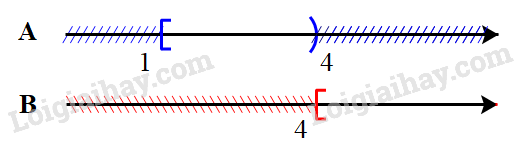
\(A \cap B = \emptyset ,A \cup B = [1; + \infty ),A{\rm{\backslash }}B = [1,4),B{\rm{\backslash }}A = [4; + \infty )\)
d) \(A = \{ x \in \mathbb{R}|1 \le x < 6\} = [1;6),B = (2;9)\)
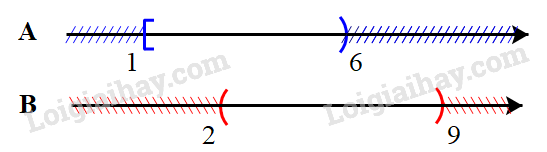
\(A \cap B = (2;6),A \cup B = [1;9),A{\rm{\backslash }}B = [1;2],B{\rm{\backslash }}A = [2;6]\)
Câu 2
Cách giải:
Gọi thời lượng công ty đặt quảng cáo trên sóng phát thanh, trên truyền hình lần lượt là x, y (phút) \((x,y \ge 0)\)
Quảng cáo trên phát thanh dài ít nhất 5 phút nên \(x \ge 5\)
Quảng cáo trên truyền hình dài nhiều nhất 4 phút nên \(0 \le y \le 4\)
Hiệu quả chung của quảng cáo là \(F = x + 6y\)
Chi phí cho quảng cáo là: 800 000.x + 4 000 000.y (đồng)
Chi tối đa 16 000 000 đồng cho quảng cáo nên \(800{\rm{ }}000.x{\rm{ }} + {\rm{ }}4{\rm{ }}000{\rm{ }}000.y \le 16\;000\;000\) hay \(x + 5y \le 20\)
Bài toán trở thành: Tìm x,y sao cho \(F = x + 6y\) đạt GTLN với các điều kiện:
\(\left\{ \begin{array}{l}x \ge 5\\0 \le y \le 4\\x + 5y \le 20\end{array} \right.\) (*)
Biểu diễn miền nghiệm của (*) trên hệ trục Oxy, ta được:
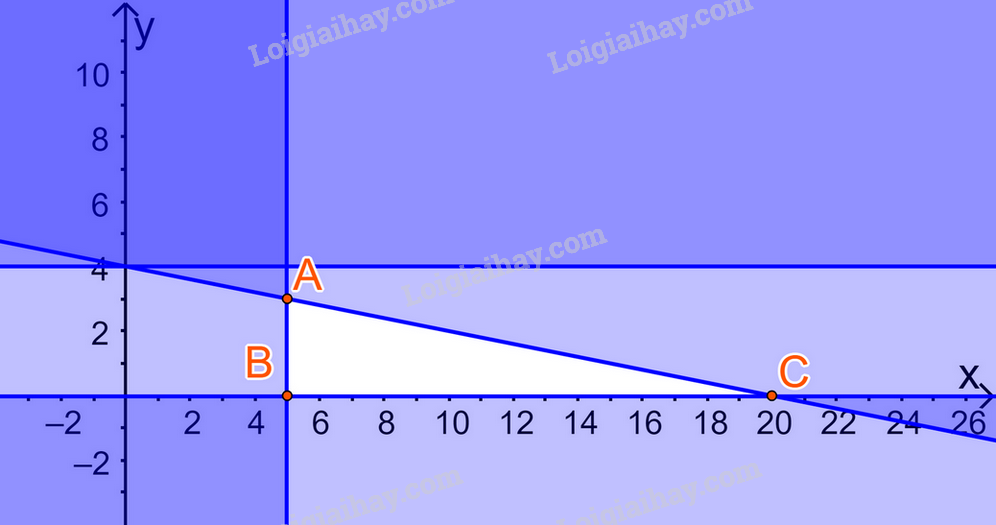
Miền nghiệm là miền tam giác ABC (kể cả các cạnh), trong đó \(A(5;3),B(5;0),C(20;0)\)
Lần lượt thay tọa độ các điểm A, B, C, D vào biểu thức \(F(x;y) = x + 6y\) ta được:
\(\begin{array}{l}F(5;3) = 5 + 6.3 = 23\\F(5;0) = 5 + 6.0 = 5\\F(20;0) = 20 + 6.0 = 20\end{array}\)
Do đó F đạt giá trị lớn nhất bằng 23 tại \(x = 5;y = 3\)
Vậy công ty đó nên đặt quảng cáo 5 phút trên sóng phát thanh và 3 phút trên truyền hình để đạt hiệu quả cao nhất.
Câu 3:
Cách giải:
a) Parabol \((P):y = a{x^2} + bx + c\) đi qua A(4;3) nên \(3 = a{.4^2} + b.4 + c \Leftrightarrow 16a + 4b + c = 3\) (*)
Lại có: (P) có đỉnh \(I(2; – 1)\)
\( \Rightarrow \left\{ \begin{array}{l}\frac{{ – b}}{{2a}} = 2\\a{.2^2} + b.2 + c = – 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4a + b = 0\\4a + 2b + c = – 1\end{array} \right.\)
Thay \(4a + b = 0\) vào (*) ta được \(4(4a + b) + c = 3 \Leftrightarrow c = 3\)
Giải hệ \(\left\{ \begin{array}{l}4a + b = 0\\4a + 2b + 3 = – 1\end{array} \right.\) ta được \(a = 1;b = – 4\)
Vậy parabol đó là \((P):y = {x^2} – 4x + 3\)
b) Parabol \((P):y = {x^2} – 4x + 3\) có \(a = 1 > 0,b = – 4\)
Bảng biến thiên
Hàm số đồng biến trên \((2; + \infty )\) và nghịch biến trên \(( – \infty ;2)\).
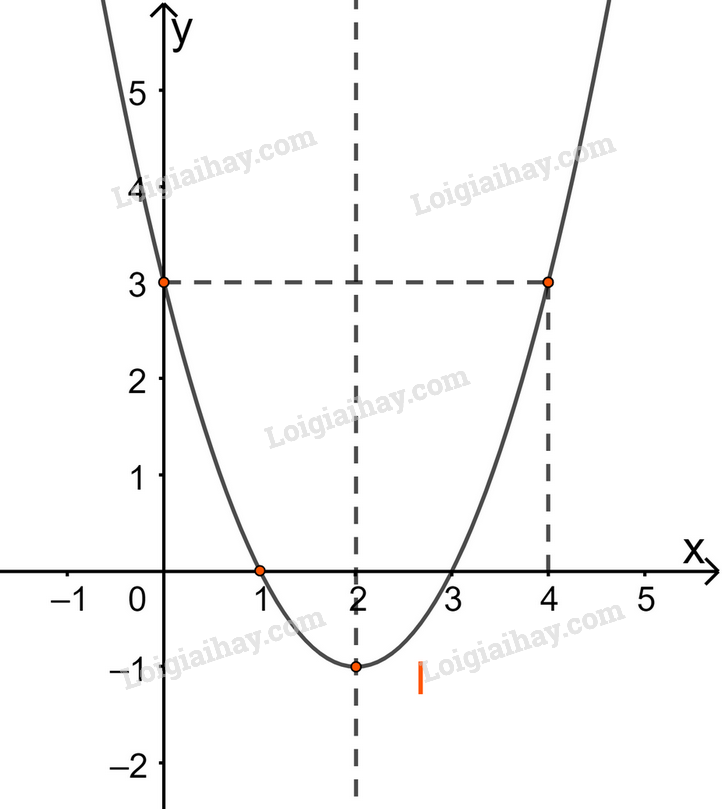
+ Vẽ đồ thị
Đỉnh \(I(2; – 1)\)
(P) giao Oy tại điểm \(A’\left( {0;3} \right)\)
(P) giao Ox tại \(B(3;0)\) và \(C(1;0)\)
Điểm \(A(4;3)\) đối xứng với \(A’\left( {0;3} \right)\) qua trục đối xứng.
Câu 4.
Cách giải:
Hàm số \(y = 3{x^2} – 6x + 7\) có \(a = 3 > 0,b = – 6 \Rightarrow – \frac{b}{{2a}} = 1;\;y(1) = 4\).
Ta có bảng biến thiên
Mà \(f( – 2) = 31,f(5) = 52,f(1) = 4\)
\( \Rightarrow \) Trên [-2;5]
Hàm số đạt GTLN bằng 52 tại \(x = 5\), đạt GTNN bằng 4 tại \(x = 1\).