Hướng dẫn giải Vận dụng 2 Bài 2. Ứng dụng của hệ phương trình bậc nhất ba ẩn (trang 15, 16, 17) – Chuyên đề học tập Toán 10 Chân trời sáng tạo. Gợi ý: Bước 1: Lập hệ phương trình.
Câu hỏi/Đề bài:
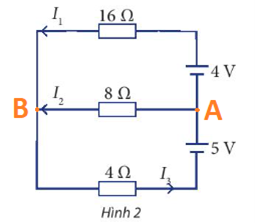
Cho sơ đồ mạch điện như Hình 2. Tính các cường độ dòng điện \({I_1},{I_2},{I_3}\)
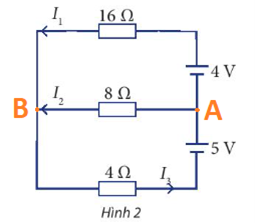
Hướng dẫn:
Bước 1: Lập hệ phương trình
+ Chọn ẩn và đặt điều kiện cho ẩn
+ Biểu diễn các đại lượng chưa biết theo ẩn và đại lượng đã biết
+ Lập các phương trình biểu thị mối quan hệ giữa các đại lượng
Bước 2: Giải hệ phương trình
Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.
Lời giải:
Ta có:
\(\left. \begin{array}{l}{U_{AB}} = – {E_1} + {I_1}{R_1} = – 4 + 16{I_1}\\{U_{AB}} = {I_2}{R_2} = 8{I_2}\\{U_{AB}} = {E_2} – {I_3}{R_3} = 5 – 4{I_3}\end{array} \right\} \Rightarrow \left\{ \begin{array}{l} – 4 + 16{I_1} = 8{I_2}\\5 – 4{I_3} = 8{I_2}\end{array} \right.\)
Tại nút B: \({I_1} + {I_2} = {I_3}\)
Từ đó ta có hệ phương trình bậc nhất ba ẩn:
\(\left\{ \begin{array}{l}16{I_1} – 8{I_2} = 4\\8{I_2} + 4{I_3} = 5\\{I_1} + {I_2} – {I_3} = 0\end{array} \right.\)
Sử dụng máy tính cầm tay, ta được \({I_1} = \frac{{11}}{{28}},{I_2} = \frac{2}{7},{I_3} = \frac{{19}}{{28}}\)
Vậy \({I_1} = \frac{{11}}{{28}}A,{I_2} = \frac{2}{7}A,{I_3} = \frac{{19}}{{28}}A\)