Hướng dẫn giải Hoạt động 2 Bài 4. Tính chất chung của ba đường conic (trang 61, 62, 63, 64) – Chuyên đề học tập Toán 10 Chân trời sáng tạo.
Câu hỏi/Đề bài:
Cho đường conic có tiêu điểm F, đường chuẩn \(\Delta \) và một điểm M là điểm nằm trên đường conic đó. Tìm mối liên hệ giữa tỉ số \(\frac{{MF}}{{d(M,\Delta )}}\) và tên gọi của đường conic đó.
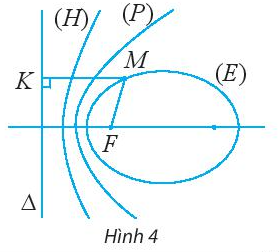
Lời giải:
+ Elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), \(M(x;y) \in (E)\)
\(\frac{{M{F_1}}}{{d(M,{\Delta _1})}} = \frac{{a + ex}}{{\frac{{a + ex}}{e}}} = e\), \(\frac{{M{F_2}}}{{d(M,{\Delta _2})}} = \frac{{a – ex}}{{\frac{{a – ex}}{e}}} = e\)
Vậy \(\frac{{M{F_1}}}{{d(M,{\Delta _1})}} = \frac{{M{F_2}}}{{d(M,{\Delta _2})}} = e = \frac{c}{a} < 1\)
+ Hypebol (H): \(\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} = 1\), \(M(x;y) \in (H)\)
\(\frac{{M{F_1}}}{{d(M,{\Delta _1})}} = \frac{{\left| {a + ex} \right|}}{{\left| {x + \frac{a}{e}} \right|}} = \frac{{\left| {a + ex} \right|}}{{\frac{{\left| {a + ex} \right|}}{e}}} = e\); \(\frac{{M{F_1}}}{{d(M,{\Delta _1})}} = \frac{{\left| {a – ex} \right|}}{{\left| {x – \frac{a}{e}} \right|}} = \frac{{\left| {a – ex} \right|}}{{\frac{{\left| {a – ex} \right|}}{e}}} = e\) ;
Vậy \(\frac{{M{F_1}}}{{d(M,{\Delta _1})}} = \frac{{M{F_2}}}{{d(M,{\Delta _2})}} = e = \frac{c}{a} > 1\)
+ Parabol (P) \({y^2} = 2px\)
\(\frac{{MF}}{{d(M,\Delta )}} = e = 1\)
Kết luận các đường conic đều có \(\frac{{MF}}{{d(M,\Delta )}} = e\) và
\(\frac{{MF}}{{d(M,\Delta )}} < 1\) thì conic là đường elip
\(\frac{{MF}}{{d(M,\Delta )}} = 1\) thì conic là đường parabol
\(\frac{{MF}}{{d(M,\Delta )}} > 1\) thì conic là đường hypebol