Giải chi tiết Giải bài 9 trang 30 Chuyên đề học tập Toán 10 – Cánh diều – Bài 1. Phương pháp quy nạp toán học – Chuyên đề học tập Toán 10 Cánh diều. Quan sát Hình 6…
Đề bài/câu hỏi:
Quan sát Hình 6
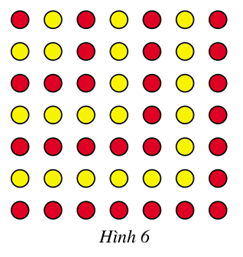
a) Nêu quy luật sắp xếp các chấm đỏ và vàng xen kẽ nhau khi xếp các chấm đó từ góc trên bên trái xuống góc dưới bên phải (tạo thành hình vuông)
b) Giả sử hình vuông thứ n có mỗi cạnh chứa n chấm. Tính tổng số chấm được xếp trong hình vuông (kể cả trên cạnh). Chứng minh kết quả đó bằng phương pháp quy nạp toán học.
Lời giải:
a) Đầu tiên xếp 1 chấm đỏ.
Xếp 3 chấm màu vàng vào phía bên phải và bên dưới chấm đỏ để tạo thành 1 hình vuông.
Xếp 5 chấm màu đỏ vào phía bên phải và bên dưới các chấm trước đó để tạo thành 1 hình vuông.
Xếp 7 chấm màu vàng vào phía bên phải và bên dưới các chấm trước đó để tạo thành 1 hình vuông.
…
Cứ như vậy, các chấm đỏ và vàng được xếp xen kẽ nhau tạo thành 1 hình vuông.
Trong đó số chấm thêm vào để tạo thành hình vuông là các số lẻ liên tiếp bắt đầu từ 1.
b) Nhận xét: Hình vuông thứ n mỗi cạnh có n chấm. Hình vuông này được tạo bởi n hàng, trong mỗi hàng có n chấm
=> Số chấm được xếp trong hình vuông (kể cả trên cạnh) là \(n.n = {n^2}\) (chấm)
Mặt khác: Theo cách xếp thì số chấm để tạo thành hình vuông thứ n là: \(1 + 3 + 5 + … + (2n – 1)\)
Ta chứng minh \(1 + 3 + 5 + … + (2n – 1) = {n^2}\) bằng phương pháp quy nạp.
Bước 1: Khi \(n = 1\) ta có \(1 = {1^2}\) hiển nhiên đúng
Như vậy đẳng thức đúng với \(n = 1\)
Bước 2: Với k là một số nguyên dương tùy ý mà đẳng thức đúng, ta phải chứng minh đẳng thức đúng với k+1, tức là:
\(1 + 3 + 5 + … + \left[ {2(k + 1) – 1} \right] = {(k + 1)^2}\) hay \(1 + 3 + 5 + … + (2k + 1) = {(k + 1)^2}\)
Thật vậy, theo giả thiết quy nạp ta có:
\(1 + 3 + 5 + … + (2k – 1) = {k^2}\)
Suy ra
\(1 + 3 + 5 + … + (2k + 1) = {k^2} + (2k + 1) = {(k + 1)^2}\)
Vậy đẳng thức đúng với k+1. Do đó, theo nguyên lí quy nạp toán học, đẳng thức đúng với mọi \(n \in \mathbb{N}*\).