Phương trình của hypebol \(\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} = 1\) trong đó \(a > 0, b > 0\). Khi đó ta có. Lời giải Giải bài 2 trang 56 Chuyên đề học tập Toán 10 – Cánh diều – Bài 2. Hypebol – Chuyên đề học tập Toán 10 Cánh diều. Trong mặt phẳng tọa độ Oxy, cho hypebol có phương trình chính tắc là \(\frac{{{x^2}}}{4} – \frac{{{y^2}}}{1} = 1\…
Đề bài/câu hỏi:
Trong mặt phẳng tọa độ Oxy, cho hypebol có phương trình chính tắc là \(\frac{{{x^2}}}{4} – \frac{{{y^2}}}{1} = 1\)
a) Xác định tọa độ các đỉnh, tiêu điểm, tiêu cự, độ dài trục thực của hypebol
b) Xác định phương trình các đường tiệm cận của hypebol và vẽ hypebol trên.
Hướng dẫn:
Phương trình của hypebol \(\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} = 1\) trong đó \(a > 0,b > 0\). Khi đó ta có:
+ Tiêu điểm \({F_1}( – c;0),{F_2}(c;0)\)
+ Các đỉnh là \({A_1}\left( { – a;0} \right),{A_2}\left( {a;0} \right)\)
+ Tiêu cự: \(2c = 2\sqrt {{a^2} + {b^2}} \)
+ Độ dài trục thực: \(2a\), độ dài trục ảo: \(2b\)
+ Hai đường tiệm cận của hypebol (H) lần lượt có phương trình \(y = – \frac{b}{a}x,y = \frac{b}{a}x\)
Lời giải:
a) Ta có: \(a = 2,b = 1 \Rightarrow c = \sqrt {{a^2} + {b^2}} = \sqrt {{2^2} + {1^2}} = \sqrt 5 \)
+ Tọa độ các đỉnh của hypebol là \({A_1}\left( { – 2;0} \right),{A_2}\left( {2;0} \right)\)
+ Tọa độ các tiêu điểm của hypebol là \({F_1}( – \sqrt 5 ;0),{F_2}(\sqrt 5 ;0)\)
+ Tiêu cự của hypebol là \(2c = 2\sqrt 5 \)
+ Độ dài trục thực: \(2a = 4\), độ dài trục ảo: \(2b = 2\)
b) Ta có phương trình các đường tiệm cận của hypebol (H) lần lượt có phương trình \(y = – \frac{1}{2}x,y = \frac{1}{2}x\)
Vẽ hypebol (H):
Ta thấy \(a = 2,b = 1\). (H) có các đỉnh \({A_1}\left( { – 2;0} \right),{A_2}\left( {2;0} \right)\)
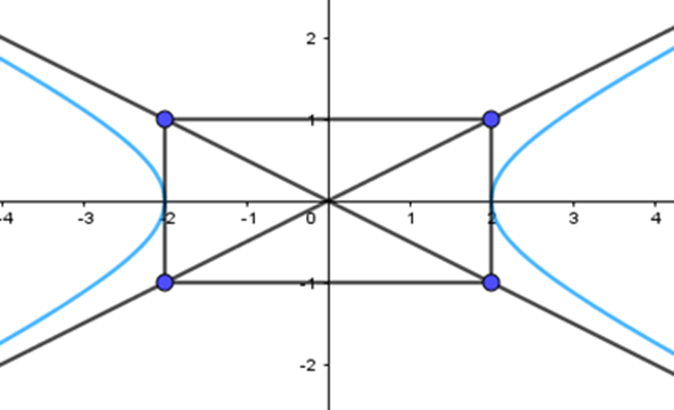
Bước 1: Vẽ hình chữ nhật cơ sở có bốn cạnh thuộc bốn thường thẳng \(x = – 2,x = 2,y = – 1,y = 1\)
Bước 2: Vẽ hai đường chéo của hình chữ nhật cơ sở
Tìm một số điểm cụ thể thuộc hypebol, chẳng hạn, ta thấy điểm \(M\left( {3;\frac{9}{4}} \right)\) thuộc (H) và điểm \({M_1}\left( {3; – \frac{9}{4}} \right),{M_2}\left( { – 3;\frac{9}{4}} \right),{M_3}\left( { – 3; – \frac{9}{4}} \right)\) thuộc (H)
Bước 3: Vẽ đường hypebol (H) bên ngoài hình chữ nhật cơ sở, nhánh bên trái tiếp xúc với cạnh của hình chữ nhật cơ sở tại điểm \({A_1}\left( { – 2;0} \right)\) và điểm \({M_2},{M_3}\); nhánh bên phải tiếp xúc với cạnh của hình chữ nhật cơ sở tại điểm \({A_2}\left( {2;0} \right)\) và điểm \(M,{M_1}\). Vẽ các điểm thuộc hypebol càng xa gốc tọa độ thì càng sát với đường tiệm cận. Hypebol nhận gốc tọa độ là tâm đối xứng và hai trục tọa độ là hai trục đối xứng.