Trả lời Câu 3 trang 98 Vở thực hành Toán 9 – Bài 13. Mở đầu về đường tròn. Gợi ý: Gọi G, K lần lượt là trung điểm của AH, BC.
Câu hỏi/Đề bài:
Cho tam giác ABC, các đường cao BD và CE cắt nhau tại H. Khẳng định nào sau đây là đúng?
A. Bốn điểm B, E, D, C cùng nằm trên một đường tròn.
B. Bốn điểm A, E, H, D cùng nằm trên một đường tròn.
C. \(DE < BC\).
D. Cả ba đáp án trên đều đúng.
Hướng dẫn:
+ Gọi G, K lần lượt là trung điểm của AH, BC.
+ Chứng minh \(GA = GE = GD = GH\) nên bốn điểm A, E, H, D thuộc đường tròn tâm (G, GA).
+ Chứng minh \(KB = KD = KE = KC\) nên bốn điểm B, E, D, C thuộc đường tròn tâm (K, KC).
+ Sử dụng quan hệ giữa cạnh và góc trong tam giác chứng minh được \(DE < BC\).
Lời giải:
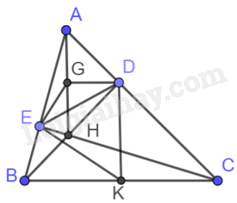
Gọi G, K lần lượt là trung điểm của AH, BC.
Vì EG là đường trung tuyến trong tam giác AEH vuông tại E nên \(EG = GH = AG\).
Vì DG là đường trung tuyến trong tam giác ADH vuông tại D nên \(DG = GH = AG\).
Do đó \(GA = GE = GD = GH\) nên bốn điểm A, E, H, D thuộc đường tròn tâm (G, GA).
Vì EK là đường trung tuyến trong tam giác BEC vuông tại E nên \(EK = BK = KC\).
Vì DK là đường trung tuyến trong tam giác BDC vuông tại D nên \(DK = BK = KC\).
Do đó \(KB = KD = KE = KC\) nên bốn điểm B, E, D, C thuộc đường tròn tâm (K, KC).
Tam giác EDC có góc EDC là góc tù nên \(ED < EC\) (quan hệ giữa cạnh và góc đối diện trong tam giác)
Tam giác BEC vuông tại E nên \(EC < BC\) (quan hệ giữa cạnh và góc đối diện trong tam giác)
Do đó, \(DE < BC\)
Chọn D