Đáp án Câu 2 trang 112 Vở thực hành Toán 9 – Bài 16. Vị trí tương đối của đường thẳng và đường tròn. Tham khảo: Chứng minh tam giác MBI vuông tại B.
Câu hỏi/Đề bài:
Cho một điểm M nằm ngoài đường tròn (I; 6cm), vẽ tiếp tuyến MB đến đường tròn đó (B là tiếp điểm). Nếu \(MI = 10cm\) thì độ dài MB bằng
A. 6 cm.
B. 8 cm.
C. 7 cm.
D. 10 cm.
Hướng dẫn:
+ Chứng minh tam giác MBI vuông tại B.
+ Áp dụng định lí Pythagore vào tam giác MBI vuông tại B ta tính được MB.
Lời giải:
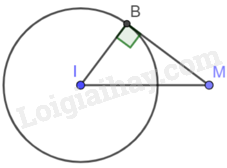
Vì MB là tiếp tuyến của (I) nên \(MB \bot IB\) tại B. Khi đó tam giác IMB vuông tại B.
Áp dụng định lí Pythagore vào tam giác MBI vuông tại B ta có:
\(I{B^2} + M{B^2} = M{I^2}\)
\(MB = \sqrt {M{I^2} – I{B^2}} = \sqrt {{{10}^2} – {6^2}} = 8\left( {cm} \right)\)
Chọn B