Trả lời Câu 2 trang 101 Vở thực hành Toán 9 – Bài 14. Cung và dây của một đường tròn. Hướng dẫn: Chứng minh tam giác AOB cân tại O.
Câu hỏi/Đề bài:
Cho đường tròn (O; R) và điểm M nằm trong đường tròn (O). Kẻ dây AB của đường tròn (O) nhận M làm trung điểm. Biết \(R = 5cm\) và \(OM = 1,4cm\). Độ dài dây AB là
A. 9,5cm.
B. 9,6cm.
C. 9,8cm.
D. 9cm.
Hướng dẫn:
+ Chứng minh tam giác AOB cân tại O, suy ra OM là đường trung tuyến đồng thời là đường cao.
+ Áp dụng định lí Pythagore vào tam giác OMB vuông tại M ta tính được MB.
+ \(AB = 2MB\).
Lời giải:
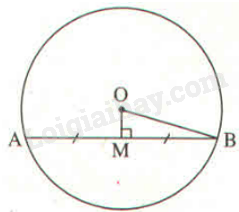
Tam giác AOB có \(OA = OB\) (bán kính (O)) nên tam giác AOB cân tại O. Do đó, OM là đường trung tuyến đồng thời là đường cao.
Áp dụng định lí Pythagore vào tam giác OMB vuông tại M có: \(M{B^2} + O{M^2} = O{B^2}\)
Suy ra \(MB = \sqrt {O{B^2} – O{M^2}} = \sqrt {{5^2} – {{1,4}^2}} = 4,8\left( {cm} \right)\)
Do đó, \(AB = 2MB = 2.4,8 = 9,6\left( {cm} \right)\)
Chọn B