Tính BC. + Tính được \(A{B^2} + A{C^2} = B{C^2}\), \(\frac{1}{2}. AB. AC\) nên tính được \({\left( {AB + AC} \right)^2}\). Hướng dẫn giải Giải bài 7 trang 97 vở thực hành Toán 9 tập 2 – . Cho tam giác ABC là tam giác vuông tại đỉnh A và nội tiếp đường tròn (O) có bán kính…
Đề bài/câu hỏi:
Cho tam giác ABC là tam giác vuông tại đỉnh A và nội tiếp đường tròn (O) có bán kính 5cm. Biết rằng diện tích tam giác ABC bằng \(24c{m^2}\). Tính bán kính đường tròn nội tiếp của tam giác ABC.
Hướng dẫn:
+ Tính BC.
+ Tính được \(A{B^2} + A{C^2} = B{C^2}\), \(\frac{1}{2}.AB.AC\) nên tính được \({\left( {AB + AC} \right)^2}\), từ đó tính được \(AB + AC\).
+ Gọi I là tâm đường tròn nội tiếp tam giác ABC và r là bán kính đường tròn nội tiếp tam giác ABC. Khi đó, r là chiều cao hạ từ đỉnh I xuống các cạnh BC, CA, AB của các tam giác BIC, CIA, AIB. Do đó
\({S_{ABC}} = {S_{BIC}} + {S_{CIA}} + {S_{AIB}} = \frac{1}{2}BC.r.\frac{1}{2}CA.r + \frac{1}{2}AB.r = \frac{1}{2}\left( {AB + AC + BC} \right).r\), từ đó tính được r.
Lời giải:
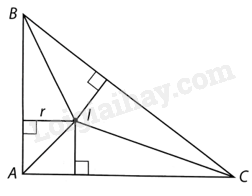
Vì bán kính đường tròn ngoại tiếp tam giác vuông bằng nửa cạnh huyền của tam giác nên \(BC = 2.5 = 10\left( {cm} \right)\).
Theo định lí Pythagore vào tam giác ABC vuông tại A, ta có: \(A{B^2} + A{C^2} = B{C^2} = 100\left( {c{m^2}} \right)\).
Vì diện tích tam giác ABC bằng \(24c{m^2}\) nên:
\(\frac{1}{2}.AB.AC = 24\left( {c{m^2}} \right)\).
Từ đây suy ra
\({\left( {AB + AC} \right)^2} = A{B^2} + 2AB.AC + A{C^2} = 196\) hay \(AB + AC = 14cm\).
Gọi I là tâm đường tròn nội tiếp tam giác ABC và r là bán kính đường tròn nội tiếp tam giác ABC. Khi đó, r là chiều cao hạ từ đỉnh I xuống các cạnh BC, CA, AB của các tam giác BIC, CIA, AIB. Do đó
\({S_{ABC}} = {S_{BIC}} + {S_{CIA}} + {S_{AIB}}\)
\(= \frac{1}{2}BC.r.\frac{1}{2}CA.r + \frac{1}{2}AB.r \)
\(= \frac{1}{2}\left( {AB + AC + BC} \right).r\).
Suy ra \(24 = \frac{1}{2}\left( {10 + 14} \right)r\), hay \(r = 2cm\).