Diện tích hình viên phân bằng diện tích hình quạt tròn ứng với cung AC trừ đi diện tích tam giác AOC. Hướng dẫn giải Giải bài 7 trang 111 vở thực hành Toán 9 – Luyện tập chung trang 107. Cho đường tròn (O), đường kính (AB = 4sqrt 3 cm)….
Đề bài/câu hỏi:
Cho đường tròn (O), đường kính \(AB = 4\sqrt 3 cm\). Điểm C thuộc đường tròn tâm O sao cho \(\widehat {AOC} = {60^o}\). Tính diện tích hình viên phân giới hạn bởi dây AC và cung nhỏ AC.
Hướng dẫn:
Diện tích hình viên phân bằng diện tích hình quạt tròn ứng với cung AC trừ đi diện tích tam giác AOC.
Lời giải:
(H.5.26)
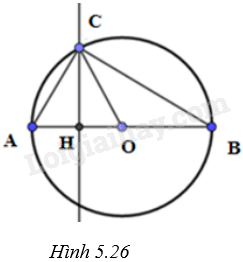
Diện tích hình quạt tròn AOC là: \({S_{AOC}} = \frac{{60}}{{360}}.\pi .{\left( {2\sqrt 3 } \right)^2} = 2\pi \left( {c{m^2}} \right)\).
Xét tam giác AOC có \(\widehat {AOC} = {60^o}\) và \(OA = OC\left( { = R} \right)\) nên tam giác AOC đều có độ dài cạnh là \(2\sqrt 3 \)cm
Gọi CH là đường cao của tam giác AOC. Khi đó, \(CH = CO.\sin {60^o} = 2\sqrt 3 .\frac{{\sqrt 3 }}{2} = 3\left( {cm} \right)\)
Diện tích tam giác AOC là: \({S_{AOC}} = \frac{1}{2}CH.AC = \frac{1}{2}.3.2\sqrt 3 = 3\sqrt 3 \left( {c{m^2}} \right)\)
Diện tích hình viên phân cần tính là: \(S = {S_{AOC}} – {S_{AOC}} = 2\pi – 3\sqrt 3 \left( {c{m^2}} \right)\)