Trong tam giác vuông ABC, ta có: \(A{C^2} = B{C^2} – A{B^2}\) suy ra AC, \(\sin B = \frac{{AC}}{{BC}}\) suy ra góc B. Vận dụng kiến thức giải Giải bài 6 trang 93 vở thực hành Toán 9 – Bài tập cuối Chương 4. Cho tam giác ABC vuông tại A, biết (AB = 6cm,BC = 11cm). a) Giải tam giác vuông ABC….
Đề bài/câu hỏi:
Cho tam giác ABC vuông tại A, biết \(AB = 6cm,BC = 11cm\).
a) Giải tam giác vuông ABC.
b) Tính độ dài đường cao AH, đường phân giác AD.
(Kết quả về cạnh làm tròn đến chữ số thập phân thứ nhất, kết quả về góc làm tròn đến độ).
Hướng dẫn:
a) Trong tam giác vuông ABC, ta có: \(A{C^2} = B{C^2} – A{B^2}\) suy ra AC, \(\sin B = \frac{{AC}}{{BC}}\) suy ra góc B, \(\widehat C = {90^o} – \widehat B\) nên tính được góc C.
b) + Trong tam giác vuông ABH, \(\sin B = \frac{{AH}}{{AB}}\) nên tính được AH.
+ Tính được góc BAD, \(\widehat {BAH} = {90^o} – \widehat B\), \(\widehat {HAD} = \widehat {BAD} – \widehat {BAH}\).
+ Trong tam giác ADH vuông tại H, ta có \(\cos \widehat {HAD} = \frac{{AH}}{{AD}}\) nên tính được AD.
Lời giải:
(H.4.45)
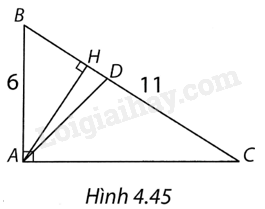
a) Trong tam giác vuông ABC, ta có
\(A{C^2} = B{C^2} – A{B^2} = {11^2} – {6^2}\), suy ra \(AC \approx 9,2\)
\(\sin B = \frac{{AC}}{{BC}} = \frac{{\sqrt {85} }}{{11}} \approx 0,84\), suy ra \(\widehat B \approx {57^o}\)
Từ đó suy ra \(\widehat C = {90^o} – \widehat B \approx {33^o}\)
b) Trong tam giác vuông ABH, ta có: \(\sin B = \frac{{AH}}{{AB}}\), suy ra \(AH = AB.\sin B \approx 5,0\)
Vì AD là đường phân giác nên \(\widehat {BAD} = \frac{1}{2}\widehat {BAC} = {45^o}\)
Trong tam giác vuông ABH, ta có \(\widehat {BAH} = {90^o} – \widehat B = {33^o}\)
Do đó, \(\widehat {HAD} = \widehat {BAD} – \widehat {BAH} = {45^o} – {33^o} = {12^o}\)
Trong tam giác ADH vuông tại H, ta có \(\cos \widehat {HAD} = \frac{{AH}}{{AD}}\), suy ra \(AD = \frac{{AH}}{{\cos \widehat {HAD}}} \approx 5,1\)