Đường thẳng \(\left( {{d_1}} \right)\) đi qua hai điểm \(A\left( {0;2} \right)\) và điểm \(B\left( {4;0} \right)\). Đường thẳng \(\left( {{d_2}} \right)\. Hướng dẫn cách giải/trả lời Giải bài 5 trang 131 vở thực hành Toán 9 tập 2 – . Kí hiệu (left( {{d_1}} right)) là đường thẳng (x + 2y = 4,…
Đề bài/câu hỏi:
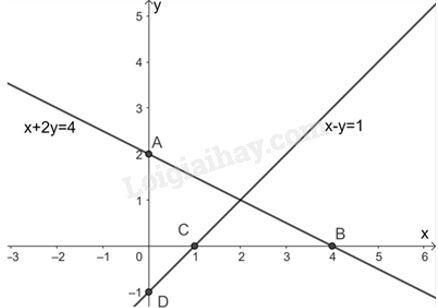
Kí hiệu \(\left( {{d_1}} \right)\) là đường thẳng \(x + 2y = 4,\left( {{d_2}} \right)\) là đường thẳng \(x – y = 1\).
a) Vẽ \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) trên cùng một mặt phẳng tọa độ.
b) Giải hệ phương trình \(\left\{ \begin{array}{l}x + 2y = 4\\x – y = 1\end{array} \right.\) để tìm tọa độ giao điểm của hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\).
Hướng dẫn:
a) Đường thẳng \(\left( {{d_1}} \right)\) đi qua hai điểm \(A\left( {0;2} \right)\) và điểm \(B\left( {4;0} \right)\).
Đường thẳng \(\left( {{d_2}} \right)\) đi qua hai điểm \(C\left( {1;0} \right)\) và \(D\left( {0; – 1} \right)\).
Biểu diễn các điểm A, B, C, D trên cùng một mặt phẳng tọa độ Oxy.
b) Giải hệ phương trình bằng phương pháp thế.
Lời giải:
a) Nhận xét:
Đường thẳng \(\left( {{d_1}} \right)\) đi qua hai điểm \(A\left( {0;2} \right)\) và điểm \(B\left( {4;0} \right)\).
Đường thẳng \(\left( {{d_2}} \right)\) đi qua hai điểm \(C\left( {1;0} \right)\) và \(D\left( {0; – 1} \right)\).
b) Xét hệ hai phương trình bậc nhất hai ẩn:
\(\left\{ \begin{array}{l}x + 2y = 4\\x – y = 1\end{array} \right.\) .
Từ phương trình thứ hai suy ra \(x = y + 1\). Thế vào phương trình thứ nhất ta được:
\(y + 1 + 2y = 4\), hay \(3y = 3\), suy ra \(y = 1\).
Từ đó tìm được \(x = 2\).
Vậy giao điểm của hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) là điểm (2; 1).