Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC. Ta có: \(R = \frac{{\sqrt 3 }}{3}BC\) nên tính được BC. Hướng dẫn cách giải/trả lời Giải bài 2 trang 92 vở thực hành Toán 9 tập 2 – . Cho tam giác đều ABC nội tiếp đường tròn (O). Biết rằng đường tròn (O) có bán kính bằng 3cm….
Đề bài/câu hỏi:
Cho tam giác đều ABC nội tiếp đường tròn (O). Biết rằng đường tròn (O) có bán kính bằng 3cm. Tính diện tích tam giác ABC.
Hướng dẫn:
+ Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC. Ta có: \(R = \frac{{\sqrt 3 }}{3}BC\) nên tính được BC.
+ Gọi M là trung điểm của BC nên \(AM = \frac{3}{2}AO\).
+ Diện tích tam giác ABC là: \(S = \frac{1}{2}AM.BC\).
Lời giải:
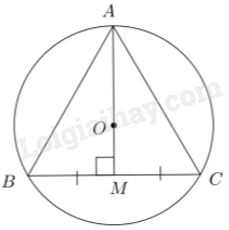
Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC. Ta có: \(R = \frac{{\sqrt 3 }}{3}BC\), hay \(BC = \sqrt 3 R = 3\sqrt 3 cm\).
Gọi M là trung điểm của BC. Ta có: \(AM = \frac{3}{2}AO = \frac{9}{2}cm\).
Vậy \({S_{ABC}} = \frac{1}{2}AM.BC = \frac{{27\sqrt 3 }}{4}\;c{m^2}\).