Áp dụng định lí Pythagore vào tam giác AHO vuông tại H để tính AH, từ đó đưa ra kết luận. Giải và trình bày phương pháp giải Giải bài 2 trang 129, 130 vở thực hành Toán 9 tập 2 – . Một vệ tinh địa tĩnh chuyển động theo quỹ đạo tròn cách bề mặt Trái Đất khoảng (AB = 36;000km),…
Đề bài/câu hỏi:
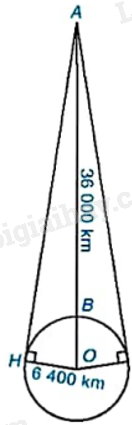
Một vệ tinh địa tĩnh chuyển động theo quỹ đạo tròn cách bề mặt Trái Đất khoảng \(AB = 36\;000km\), tâm quỹ đạo trùng với tâm O của Trái Đất như hình bên. Vệ tinh phát tín hiệu vô tuyến theo đường thẳng đến một số vị trí trên bề mặt Trái Đất. Cho biết bán kính Trái Đất khoảng 6 400km, vị trí xa nhất trên bề mặt Trái Đất có thể nhận được tín hiệu từ vệ tinh cách vệ tinh bao nhiêu kilômét? (Làm tròn kết quả đến hàng đơn vị).
Hướng dẫn:
Áp dụng định lí Pythagore vào tam giác AHO vuông tại H để tính AH, từ đó đưa ra kết luận.
Lời giải:
Giả sử vị trí xa nhất trên bề mặt Trái Đất nhận được tín hiệu từ vệ tinh là điểm H. Khi đó AH là tiếp tuyến của bề mặt Trái Đất.
Khoảng cách giữa vệ tinh và tâm Trái Đất là \(AO = AB + BO = 36\;000 + 6\;400 = 42\;400\left( {km} \right)\).
Vì AH là tiếp tuyến của bề mặt Trái Đất nên \(\Delta AOH\) vuông tại H.
Áp dụng định lí Pythagore cho tam giác AHO vuông tại H, ta có:
\(A{O^2} = A{H^2} + H{O^2}\)
\(A{H^2} = A{O^2} – H{O^2} = 42\;{400^2} – 6\;{400^2} = 1\;756\;800\;000\)
\(AH = \sqrt {1\;756\;800\;000} \approx 41\;914\left( {km} \right)\).
Vậy vị trí xa nhất trên Trái Đất có thể nhận tín hiệu của vệ tinh cách vệ tinh khoảng 41 914km.