Lời giải Câu hỏi Vận dụng trang 70 SGK Toán 9 Kết nối tri thức – Bài 27. Góc nội tiếp. Tham khảo: Theo định lí Pythagore đảo chứng minh được tam giác BOC vuông tại O, tính được góc BOC.
Câu hỏi/Đề bài:
Trở lại tình huống mở đầu, hãy tính số đo của góc BAC nếu đường tròn có bán kính 2cm và dây cung \(BC = 2\sqrt 2 cm\).
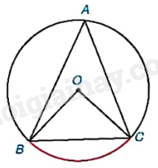
Chúng ta đã biết số đo góc ở tâm BOC của đường tròn (O) trong Hình 9.1 bằng số đo của cung bị chắn.
Hướng dẫn:
+ Theo định lí Pythagore đảo chứng minh được tam giác BOC vuông tại O, tính được góc BOC.
+ Vì góc BOC và góc BAC lần lượt là góc ở tâm và góc nội tiếp cùng chắn cung BC của đường tròn (O) nên \(\widehat {BAC} = \frac{1}{2}\widehat {BOC}\).
Lời giải:
Vì B, C thuộc đường tròn (O) nên \(OB = OC = 2cm\).
Xét tam giác BOC có: \(O{B^2} + O{C^2} = B{C^2}\left( {do\;{2^2} + {2^2} = {{\left( {2\sqrt 2 } \right)}^2}} \right)\) nên tam giác BOC vuông tại O (định lí Pythagore đảo).
Suy ra, \(\widehat {BOC} = {90^o}\)
Vì góc BOC và góc BAC lần lượt là góc ở tâm và góc nội tiếp cùng chắn cung BC của đường tròn (O) nên \(\widehat {BAC} = \frac{1}{2}\widehat {BOC} = \frac{1}{2}{.90^o} = {45^o}\).