Câu hỏi trang 77: Hãy nêu cách giải tam giác ABC vuông tại A khi biết hai cạnh AB = c, AC = b hoặc AB = c, BC = a

Câu hỏi/Đề bài:

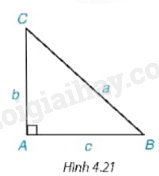
1. Hãy nêu cách giải tam giác ABC vuông tại A khi biết hai cạnh \(AB = c,AC = b\) hoặc \(AB = c,BC = a\) và không sử dụng định lý Pythagore (H.4.21).

2. Hãy nêu cách giải tam giác ABC vuông tại A khi biết cạnh góc vuông AB (hoặc cạnh huyền BC) và góc B.

Hướng dẫn:

Để giải tam giác vuông ngoài sử dụng định lý Pythagore ta có thể sử dụng tỉ số lượng giác.

Lời giải:

1. Trường hợp biết \(AB = c,AC = b\)

Tam giác ABC vuông tại A nên ta có: \(\tan \widehat B = \frac{b}{c}\) từ đó ta tính được góc B, và tính được góc C thông qua định lý tổng ba góc trong một tam giác. Sau khi tính được góc B, ta dùng tỉ số lượng giác \(\cos \widehat B = \frac{c}{{CB}}\) từ đó ta tính được \(CB = \frac{c}{{\cos \widehat B}}\)

Trường hợp \(AB = c,BC = a\)

Tam giác ABC vuông tại A nên ta có: \(\cos \widehat B = \frac{b}{c}\) từ đó ta tính được góc B, và tính được góc C thông qua định lý tổng ba góc trong một tam giác. Sau khi tính được góc B, ta dùng tỉ số lượng giác \(\tan \widehat B = \frac{{AC}}{c}\) từ đó ta tính được \(AC = c.\tan \widehat B\)

2. Tam giác ABC vuông tại A khi biết cạnh góc vuông AB (hoặc cạnh huyền BC) và góc B.

Trường hợp biết cạnh góc vuông AB và góc B

Biết góc B ta tính được góc C thông qua định lý tổng ba góc trong một tam giác. Để tính cạnh BC ta dùng tỉ số lượng giác \(\cos \widehat B = \frac{c}{{BC}}\) từ đó ta tính được \(BC = \frac{c}{{\cos \widehat B}}\) và tỉ số lượng giác \(\tan \widehat B = \frac{{AC}}{c}\) từ đó ta tính được \(AC = c.\tan \widehat B\)

Trường hợp biết cạnh huyền BC và góc B

Biết góc B ta tính được góc C thông qua định lý tổng ba góc trong một tam giác. Để tính cạnh AB ta dùng tỉ số lượng giác \(\cos \widehat B = \frac{{AB}}{a}\) từ đó ta tính được \(AB = a.\cos \widehat B\) và tỉ số lượng giác \(\sin \widehat B = \frac{{AC}}{a}\) từ đó ta tính được \(AC = a.\sin \widehat B\)