Giải chi tiết Câu hỏi Thực hành 3 trang 114 SGK Toán 9 Kết nối tri thức – Giải phương trình – hệ phương trình và vẽ đồ thị hàm số với phần mềm GeoGebra. Gợi ý: Khởi động GeoGebra và chọn đồng thời hai chế độ Graphic 2 và CAS để vẽ đồ thị của.
Câu hỏi/Đề bài:
Cho đường thẳng \(\left( d \right):y = 2x + \sqrt 3 \) và parabol \(\left( P \right):y = {x^2}\).
a) Vẽ đường thẳng (d) và parabol (P) trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của (d) và (P).
Hướng dẫn:
– Khởi động GeoGebra và chọn đồng thời hai chế độ Graphic 2 và CAS để vẽ đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) và hàm số bậc nhất \(y = ax + b\left( {a \ne 0} \right)\)
+ Nhập công thức hàm số \(y = a{x^2}\) và \(y = ax + b\) vào từng ô lệnh trong cửa sổ CAS.
+ Nháy chuột chọn nút  ở đầu mỗi ô lệnh để vẽ đồ thị hàm số trong cửa sổ Graphic 2.
ở đầu mỗi ô lệnh để vẽ đồ thị hàm số trong cửa sổ Graphic 2.
– Sử dụng câu lệnh Intersect ({ , (}) trên ô lệnh của cửa sổ CAS để tìm tọa độ giao điểm của hai đường thẳng có phương trình tương ứng.
Lời giải:
a) Nhập
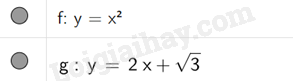
Ta được đồ thị
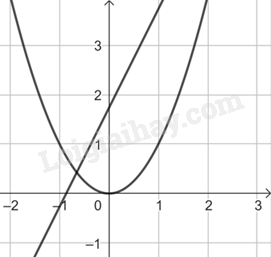
b)
