Chứng minh rằng các cọc gôn, vị trí đặt bóng đều thuộc đường tròn có tâm là điểm phạt đền. Trả lời Giải bài tập 9.6 trang 71 SGK Toán 9 tập 2 – Kết nối tri thức – Bài 27. Góc nội tiếp. Trên sân bóng, khi trái bóng được đặt tại điểm phạt đền thì có góc sút bằng ({36^o}) và trái…
Đề bài/câu hỏi:
Trên sân bóng, khi trái bóng được đặt tại điểm phạt đền thì có góc sút bằng \({36^o}\) và trái bóng cách mỗi cọc gôn 11,6m (H.9.11). Hỏi khi trái bóng đặt ở vị trí cách điểm phạt đền 11,6m thì góc sút bằng bao nhiêu?

Hướng dẫn:
+ Chứng minh rằng các cọc gôn, vị trí đặt bóng đều thuộc đường tròn có tâm là điểm phạt đền.
+ Sử dụng liên hệ giữa góc ở tâm và góc nội tiếp cùng chắn một cung trong một đường tròn để tính góc sút phạt.
Lời giải:
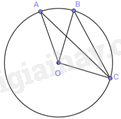
Gọi A, B lần lượt là các cọc gôn, C là vị trí đặt bóng, O là chấm phạt đền.
Theo đề bài ta có: \(OA = OB = OC = 11,6m\) nên A, B, C thuộc đường tròn tâm O.
Vì góc nội tiếp ACB và góc ở tâm AOB cùng chắn cung nhỏ AB của đường tròn (O) nên \(\widehat {ACB} = \frac{1}{2}\widehat {AOB} = \frac{1}{2}{.36^o} = {18^o}\)
Vậy khi trái bóng cách vị trí phạt đền 11,6m thì góc sút bằng \({18^o}\).