Gọi tám cabin tạo thành một bát giác đều BACDEFGH nội tiếp đường tròn (O). Hướng dẫn giải Giải bài tập 9.30 trang 89 SGK Toán 9 tập 2 – Kết nối tri thức – Bài 30. Đa giác đều. Cho vòng quay mặt trời gồm tám cabin như Hình 9.55….
Đề bài/câu hỏi:
Cho vòng quay mặt trời gồm tám cabin như Hình 9.55. Hỏi để cabin A di chuyển đến vị trí cao nhất thì vòng quay phải quay thuận chiều kim đồng hồ quanh tâm bao nhiêu độ?
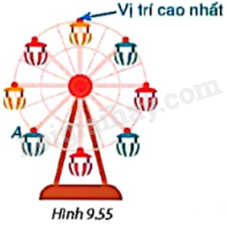
Hướng dẫn:
+ Gọi tám cabin tạo thành một bát giác đều BACDEFGH nội tiếp đường tròn (O).
+ Chứng minh \(\Delta HOB = \Delta HOG = \Delta FOG = \Delta FOE = \Delta DOE = \Delta DOC = \Delta AOC = \Delta AOB\left( {c.c.c} \right)\), suy ra: \(\widehat {HOB} = \widehat {HOG} = \widehat {GOF} = \widehat {EOF} = \widehat {DOE} = \widehat {COD} = \widehat {AOC} = \widehat {AOB} = \frac{{{{360}^o}}}{8} = {45^o}\)
+ Tính góc AOG
+ Để cabin A di chuyển đến vị trí cao nhất (vị trí cabin G) thì vòng quay phải quay theo chiều thuận kim đồng hồ quanh tâm góc \({135^o}\).
Lời giải:
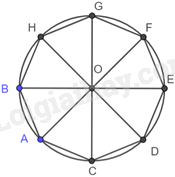
Gọi tám cabin tạo thành một bát giác đều BACDEFGH nội tiếp đường tròn (O).
Vì BACDEFGH là bát giác đều nên
\(AB = AC = CD = DE = EF = FG = GH = HB\)
Vì BACDEFGH là bát giác nội tiếp đường tròn (O) nên
\(OA = OB = OC = OD = OE = OF = OH = OG\)
Do đó
\(\Delta HOB = \Delta HOG = \Delta FOG = \Delta FOE = \Delta DOE = \Delta DOC = \Delta AOC = \Delta AOB\left( {c.c.c} \right)\)
Suy ra
\(\widehat {HOB} = \widehat {HOG} = \widehat {GOF} = \widehat {EOF} = \widehat {DOE} = \widehat {COD} = \widehat {AOC} = \widehat {AOB} = \frac{{{{360}^o}}}{8} = {45^o}\)
Ta có:
\(\widehat {AOG} = \widehat {AOB} + \widehat {BOH} + \widehat {HOG} = {45^o} + {45^o} + {45^o} = {135^o}\)
Để cabin A di chuyển đến vị trí cao nhất (vị trí cabin G) thì vòng quay phải quay theo chiều thuận kim đồng hồ quanh tâm góc \({135^o}\).