Đường tròn nội tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác đó và bán kính bằng \(\frac{{\sqrt 3 }}{6}a\). Giải và trình bày phương pháp giải Giải bài tập 9.14 trang 79 SGK Toán 9 tập 2 – Kết nối tri thức – Luyện tập chung trang 78. Cho ABC là tam giác đều có cạnh bằng 4cm….
Đề bài/câu hỏi:
Cho ABC là tam giác đều có cạnh bằng 4cm. Tính bán kính đường tròn ngoại tiếp và bán kính đường tròn nội tiếp tam giác ABC.
Hướng dẫn:
+ Đường tròn nội tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác đó và bán kính bằng \(\frac{{\sqrt 3 }}{6}a\).
+ Đường tròn ngoại tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác đó và bán kính bằng \(\frac{{\sqrt 3 }}{3}a\).
Lời giải:
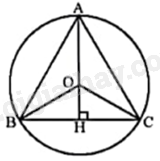
Vẽ đường tròn (O) ngoại tiếp tam giác ABC.
Vẽ đường cao AH của tam giác ABC. Tam giác ABC đều nên AH đồng thời là đường trung trực, đường trung tuyến, đường phân giác của tam giác ABC.
Vì tam giác ABC đều nên tâm O của đường tròn ngoại tiếp tam giác ABC, vừa là trọng tâm của tam giác vừa là giao điểm của ba đường phân giác. Do đó, O là tâm đường tròn nội tiếp tam giác ABC.
Do đó, OA và OH lần lượt là bán kính đường tròn ngoại tiếp và bán kính đường tròn nội tiếp \(\Delta \)ABC.
Bán kính đường tròn ngoại tiếp \(\Delta \)ABC là:
\(OA = \frac{{BC\sqrt 3 }}{3} = \frac{{4\sqrt 3 }}{3}\left( {cm} \right)\).
Bán kính đường tròn nội tiếp \(\Delta \)ABC là:
\(OH = \frac{{BC\sqrt 3 }}{6} = \frac{{4\sqrt 3 }}{6} = \frac{{2\sqrt 3 }}{3}\left( {cm} \right)\).