Thay \(x = 3;y = 3\) vào hàm số \(y = a{x^2}\) để tìm a. Hướng dẫn giải Giải bài tập 6.46 trang 30 SGK Toán 9 tập 2 – Kết nối tri thức – Bài tập cuối chương 6. Cho hàm số (y = a{x^2}). Xác định hệ số a, biết đồ thị hàm số đi qua điểm A(3;…
Đề bài/câu hỏi:
Cho hàm số \(y = a{x^2}\). Xác định hệ số a, biết đồ thị hàm số đi qua điểm A(3; 3). Vẽ đồ thị của hàm số trong trường hợp đó.
Hướng dẫn:
– Thay \(x = 3;y = 3\) vào hàm số \(y = a{x^2}\) để tìm a.
– Cách vẽ đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\):
+ Lập bảng ghi một số cặp giá trị tương ứng của x và y.
+ Trong mặt phẳng tọa độ Oxy, biểu diễn các cặp điểm (x; y) trong bảng giá trị trên và nối chúng lại để được một đường cong là đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\).
Lời giải:
Đồ thị hàm số đi qua điểm A(3; 3) nên ta có: \(3 = a{.3^2} \Rightarrow a = \frac{1}{3}\). Do đó, hàm số cần tìm là: \(y = \frac{1}{3}{x^2}\).
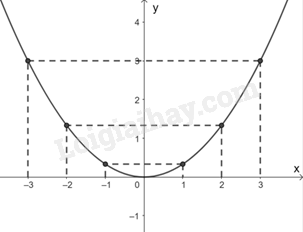
Vẽ đồ thị hàm số \(y = \frac{1}{3}{x^2}\):
Lập bảng một số cặp giá trị tương ứng của x và y:

Biểu diễn các điểm \(\left( { – 3;3} \right),\left( { – 2;\frac{4}{3}} \right);\left( { – 1;\frac{1}{3}} \right);\left( {0;0} \right);\left( {1;\frac{1}{3}} \right),\left( {2;\frac{4}{3}} \right);\left( {3;3} \right)\) trên mặt phẳng tọa độ Oxy và nối chúng lại ta được đồ thị hàm số \(y = \frac{1}{3}{x^2}\) như hình vẽ.