Áp dụng tính chất của hai tiếp tuyến cắt nhau. b) Gọi K là giao điểm của AN và OQ. Hướng dẫn giải Giải bài tập 5.30 trang 110 SGK Toán 9 tập 1 – Kết nối tri thức – Luyện tập chung trang 108. Cho đường tròn (O) đường kính AB, tiếp tuyến xx’ tại A và tiếp tuyến yy’ tại B của (O)….
Đề bài/câu hỏi:
Cho đường tròn (O) đường kính AB, tiếp tuyến xx’ tại A và tiếp tuyến yy’ tại B của (O). Một tiếp tuyến thứ ba của (O) tại điểm P (khác A và B) cắt xx’ tại M và cắt yy’ tại N.
a) Chứng minh rằng MN = MA + NB.
b) Đường thẳng đi qua O và vuông góc với AB cắt NM tại Q. Chứng minh rằng Q là trung điểm của đoạn MN.
c) Chứng minh rằng AB tiếp xúc với đường tròn đường kính MN.
Hướng dẫn:
a) Áp dụng tính chất của hai tiếp tuyến cắt nhau.
b) Gọi K là giao điểm của AN và OQ, áp dụng tính chất đường trung bình cho hai tam giác ABN và AMN.
c) Áp dụng tính chất đường trung bình và câu a suy ra
\({\rm{OQ}} = \frac{1}{2}{\rm{MN}}\)nên O thuộc đường tròn đường kính MN, từ đó ta có AB là tiếp tuyến tại M.
Lời giải:
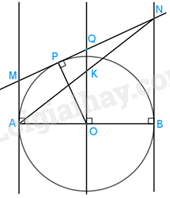
a) MA và MP là hai tiếp tuyến cắt nhau của (O) nên MA = MP
NB và NP là hai tiếp tuyến cắt nhau của (O) nên NB = NP
Ta có: MN = MP + NP = MA + NB
b) Gọi K là giao điểm của AN và OQ.
Ta có: \({\rm{BN//OK}}\) (vì cùng vuông góc với AB) và O là trung điểm của AB.
Suy ra OK là đường trung bình của tam giác ABN.
Do đó K là trung điểm của AN.
Lại có: \({\rm{AM//QK}}\) (vì cùng vuông góc với AB) và K là trung điểm của AN.
Suy ra QK là đường trung bình của tam giác AMN.
Do đó Q là trung điểm của MN.
c) OK là đường trung bình của tam giác ABN nên \({\rm{OK}} = \frac{1}{2}{\rm{NB}}\)
QK là đường trung bình của tam giác AMN nên \({\rm{QK}} = \frac{1}{2}{\rm{MA}}\)
Suy ra: \({\rm{OQ}} = {\rm{OK}} + {\rm{QK}} = \frac{1}{2}{\rm{NB}} + \frac{1}{2}{\rm{MA}} = \frac{1}{2}{\rm{MN}}\)
hay \({\rm{OQ}} = {\rm{AQ}} = {\rm{BQ}}\)
Do đó O thuộc đường tròn đường kính MN.
Mà OQ vuông góc với AB tại O nên AB là tiếp của đường tròn đường kính MN.