Vẽ đường tròn \(\left( {O;\sqrt 5 } \right)\) và các điểm M (0; 2), N (0; -3) và P(2; -1). Gợi ý giải Giải bài tập 5.1 trang 86 SGK Toán 9 tập 1 – Kết nối tri thức – Bài 13. Mở đầu về đường tròn. Trong mặt phẳng tọa độ Oxy, cho các điểm M (0 ; 2), N (0; -3) và P(2; -1)….
Đề bài/câu hỏi:
Trong mặt phẳng tọa độ Oxy, cho các điểm M (0 ; 2), N (0; -3) và P(2; -1). Vẽ hình và cho biết trong các điểm đã cho, điểm nào nằm trên, điểm nào nằm trong, điểm nào nằm ngoài đường tròn \(\left( {O;\sqrt 5 } \right)\)? Vì sao?
Hướng dẫn:
Vẽ đường tròn \(\left( {O;\sqrt 5 } \right)\) và các điểm M (0; 2), N (0; -3) và P(2; -1). Sau đó dựa vào hình vẽ xác định điểm nào nằm trên, điểm nào nằm trong, điểm nào nằm ngoài đường tròn \(\left( {O;\sqrt 5 } \right)\).
Lời giải:
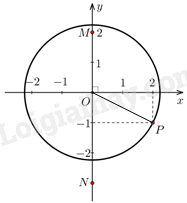
Vì \(OM = 2 < \sqrt 5 = R\) nên điểm M nằm trong đường tròn.
Vì OP là đường chéo của tam giác vuông có cạnh là 1 và 2 nên \(OP = \sqrt{1^2+2^2} = \sqrt 5 = R\) nên P nằm trên đường tròn.
Vì \(ON = 3 > \sqrt 5 = R\) nên điểm N nằm ngoài đường tròn.