Bài tập 4.8 trang 78 Toán 9 tập 1 – Kết nối tri thức: Giải tam giác ABC vuông tại A có BC = a, AC = b, AB = c, trong các trường hợp: a) a = 21, b = 18; b) b = 10

Đề bài/câu hỏi:

Giải tam giác ABC vuông tại A có \(BC = a,AC = b,AB = c,\) trong các trường hợp:

a) \(a = 21,b = 18;\)

b) \(b = 10,\widehat C = {30^0};\)

c) \(c = 5,b = 3.\)

Hướng dẫn:

Dựa vào tỉ số lượng giác giữa các cạnh ta tính được góc B hoặc góc C, và các biểu thức liên quan giữa cạnh và góc chưa biết kết hợp thêm định lý Pythagore để tính cạnh còn lại khi biết hai cạnh.

Lời giải:

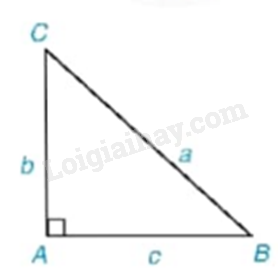
a) \(a = 21,b = 18;\)

Tam giác ABC vuông tại A, ta có: \(A{B^2} + A{C^2} = B{C^2}\) (định lý Pythagore)

Thay số ta có: \(A{B^2} + {18^2} = {21^2}\) hay \(AB = \sqrt {{{21}^2} – {{18}^2}} = 3\sqrt {13} \) (vì \(AB > 0\))

Ta có \(\sin \widehat B = \frac{{AC}}{{BC}} = \frac{{18}}{{21}} = \frac{6}{7}\) nên \(\widehat B \approx {59^0}\)

Mà \(\widehat B + \widehat C = {90^0}\) nên \(\widehat C = {90^0} – \widehat B \approx {90^0} – {59^0} = {31^0}\)

b) \(b = 10,\widehat C = {30^0};\)

Tam giác ABC vuông tại A, ta có \(\tan \widehat C = \frac{{AB}}{{AC}}\) hay \(\tan {30^0} = \frac{{AB}}{{10}}\) suy ra \(AB = 10.{{\tan {{30}^0}}} = \frac{10\sqrt 3}{3} \)

\(\cos \widehat C = \frac{{AC}}{{BC}}\) hay \(\cos{30^0} = \frac{{10}}{{BC}}\) suy ra \(BC = \frac{{10}}{{\cos {{30}^0}}} = \frac{{20\sqrt 3}}{{3}}\)

Mà \(\widehat B + \widehat C = {90^0}\) nên \(\widehat C = {90^0} – \widehat B = {90^0} – {30^0} = {60^0}\)

c) \(c = 5,b = 3.\)

Tam giác ABC vuông tại A, ta có: \(A{B^2} + A{C^2} = B{C^2}\) (định lý Pythagore)

Thay số ta có: \(B{C^2} = {5^2} + {3^2} = 34\) hay \(BC = \sqrt {34} \) (vì \(BC > 0\))

Ta có \(\sin \widehat B = \frac{{AC}}{{BC}} = \frac{3}{{\sqrt {34} }}\) nên \(\widehat B \approx {31^0}\)

Mà \(\widehat B + \widehat C = {90^0}\) nên \(\widehat C = {90^0} – \widehat B \approx {90^0} – {31^0} = {59^0}\)