Góc giữa cạnh ngắn hơn và đường chéo của hình chữ nhật chính là góc nhọn trong tam giác vuông khi biết cạnh đối và. Gợi ý giải Giải bài tập 4.4 trang 73 SGK Toán 9 tập 1 – Kết nối tri thức – Bài 11. Tỉ số lượng giác của góc nhọn. Cho hình chữ nhật có chiều dài và chiều rộng lần lượt là 3 và (sqrt 3 ….
Đề bài/câu hỏi:
Cho hình chữ nhật có chiều dài và chiều rộng lần lượt là 3 và \(\sqrt 3 .\) Tính góc giữa đường chéo và cạnh ngắn hơn của hình chữ nhật (sử dụng bảng giá trị lượng giác trang 69) .
Hướng dẫn:
Góc giữa cạnh ngắn hơn và đường chéo của hình chữ nhật chính là góc nhọn trong tam giác vuông khi biết cạnh đối và cạnh kề, ta sử dụng tỉ số lượng giác \(\tan ,\cot \)
Lời giải:
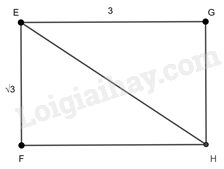
Xét hình chữ nhật EFHG có \(EG = FH = 3;EF = GH = \sqrt 3 \)
Góc giữa đường chéo và cạnh ngắn hơn là góc FEH
Ta có: \(\tan \widehat {FEH} = \frac{{FH}}{{EF}} = \frac{3}{{\sqrt 3 }} = \sqrt 3 \) nên \(\widehat {FEH} = {60^0}\)
Vậy góc giữa đường chéo và cạnh ngắn hơn là \({60^0}.\)