Cuốn sách có dạng hình chữ nhật, để tính tỉ số lượng giác \(\sin \alpha , \cos \alpha \. Giải và trình bày phương pháp giải Giải bài tập 4.14 trang 80 SGK Toán 9 tập 1 – Kết nối tri thức – Luyện tập chung trang 79. Một cuốn sách khổ (17 times 24) cm, tức là chiều rộng 17 cm, chiều dài 24 cm….
Đề bài/câu hỏi:
Một cuốn sách khổ \(17 \times 24\) cm, tức là chiều rộng 17 cm, chiều dài 24 cm. Gọi \(\alpha \) là góc giữa đường chéo và cạnh 17 cm. Tính \(\sin \alpha ,\cos \alpha \) (làm tròn đến chữ số thập phân thứ hai) và tính số đo \(\alpha \) (làm tròn đến độ) .
Hướng dẫn:
Cuốn sách có dạng hình chữ nhật, để tính tỉ số lượng giác \(\sin \alpha ,\cos \alpha \) liên quan đến đường chéo của hình chữ nhật, ta sử dụng định lý Pytagore để tính.
Chú ý: Tỉ số giữa cạnh đối và cạnh huyền gọi là sin của góc \(\alpha \), kí hiệu \(\sin \alpha \)
Tỉ số giữa cạnh kề và cạnh huyền gọi là cosin của góc \(\alpha \), kí hiệu \(\cos \alpha \)
Lời giải:
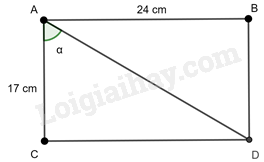
Xét cuốn sách có dạng là hình chữ nhật chiều dài \(AB = CD = 24\) cm; chiều rộng \(AC = BD = 17\) cm.
Tam giác ACD vuông tại C có \(A{D^2} = A{C^2} + C{D^2}\) (định lý Pythagore)
Thay số ta có: \(A{D^2} = {17^2} + {24^2} = 865\) hay \(AD = \sqrt {865} \) cm (vì \(AD > 0\))
\(\sin \alpha = \frac{{CD}}{{AD}} = \frac{{24}}{{\sqrt {865} }} \approx 0,82;\cos \alpha = \frac{{AC}}{{AD}} = \frac{{17}}{{\sqrt {865} }} \approx 0,58\) và \(\alpha \approx {55^0}\)