Bán kính hai nửa hình cầu là \(\frac{{1, 8}}{2} = 0, 9\left( m \right)\). + Tính thể tích \({V_1}\) hình trụ chiều cao 3. Gợi ý giải Giải bài tập 10.15 trang 107 SGK Toán 9 tập 2 – Kết nối tri thức – Luyện tập chung trang 106. Một bồn chứa xăng gồm hai nửa hình cầu có đường kính bằng 1,…
Đề bài/câu hỏi:
Một bồn chứa xăng gồm hai nửa hình cầu có đường kính bằng 1,8m và một hình trụ có chiều cao bằng 3,6m (H.10.32). Tính thể tích của bồn chứa xăng (làm tròn kết quả đến hàng phần trăm của \({m^3}\)).
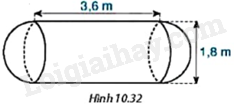
Hướng dẫn:
+ Bán kính hai nửa hình cầu là \(\frac{{1,8}}{2} = 0,9\left( m \right)\).
+ Tính thể tích \({V_1}\) hình trụ chiều cao 3,6m và bán kính 0,9m.
+ Tính thể tích \({V_2}\) hai nửa hình cầu bán kính 0,9m.
+ Thể tích bồn chứa xăng: \(V = {V_1} + {V_2}\).
Lời giải:
Bán kính hai nửa hình cầu là \(\frac{{1,8}}{2} = 0,9\left( m \right)\).
Thể tích hình trụ chiều cao 3,6m và bán kính 0,9m là:
\({V_1} = \pi .0,{9^2}.3,6 = 2,916\pi \left( {{m^3}} \right)\).
Thể thể tích hai nửa hình cầu bán kính 0,9m là:
\({V_2} = \frac{4}{3}.\pi .0,{9^3} = 0,972\pi \left( {{m^3}} \right)\).
Thể tích bồn chứa xăng là:
\(V = {V_1} + {V_2} = 2,916\pi + 0,972\pi = 3,888\pi \approx 12,21\left( {{m^3}} \right)\).