Trả lời Câu hỏi Vận dụng 2 trang 71 SGK Toán 9 Chân trời sáng tạo – Bài 2. Tứ giác nội tiếp. Hướng dẫn: Dựa vào: Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng 180o.
Câu hỏi/Đề bài:
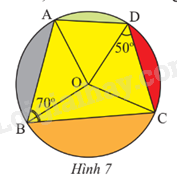
Trong hình vẽ minh họa của học sinh có một tứ giác ABCD nội tiếp đường tròn tâm O (Hình 7). Cho biết \(\widehat {ABC}\) = 70o, \(\widehat {OCD}\) = 50o. Tìm góc \(\widehat {AOD}\).
Hướng dẫn:
Dựa vào: Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng 180o.
Lời giải:
Tứ giác ABCD là tứ giác nội tiếp.
Do đó \(\widehat {ABC} + \widehat {ADC} = {180^o}\) suy ra \(\widehat {ADC} = {180^o} – \widehat {ABC} = {180^o} – {70^o} = {110^o}\).
Mà \(\widehat {ADO} + \widehat {OCD} = \widehat {ADC}\) suy ra \(\widehat {ADO} = {110^o} – {50^o} = {60^o}\).
Vì OA = OD = R nên tam giác OAD cân tại O
Suy ra \(\widehat {OAD} = \widehat {ADO} = {60^o}\) (tính chất tam giác cân)
Vậy tam giác OAD đều suy ra \(\widehat {AOD} = {60^o}\).