Giải Câu hỏi Vận dụng 1 trang 54 SGK Toán 9 Chân trời sáng tạo – Bài 4. Biến đổi đơn giản biểu thức chứa căn thức bậc hai. Hướng dẫn: Dựa vào công thức diện tích hình chữ nhật S = a. b (a: chiều dài; b: chiều rộng).
Câu hỏi/Đề bài:
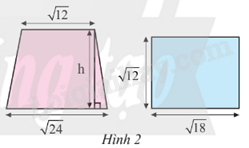
Biết rằng hình thang và hình chữ nhật ở Hình 2 có diện tích bằng nhau. Tính chiều cao h của hình thang.
Hướng dẫn:
Dựa vào công thức diện tích hình chữ nhật S = a.b (a: chiều dài; b: chiều rộng), diện tích hình thang S = \(\frac{1}{2}(a + b).h\) (a và b: chiều dài hai cạnh đáy; h: chiều cao).
Lời giải:
Ta có diện tích hình chữ nhật là: \(\sqrt {12} .\sqrt {18} = \sqrt {12.18} = \sqrt {216} = 6\sqrt 6 \)
Ta có diện tích hình thang bằng diện tích hình chữ nhật là: \(6\sqrt 6 \)
Mà diện tích hình thang là: \(\frac{1}{2}(\sqrt {12} + \sqrt {24} ).h\) = \(6\sqrt 6 \)
Suy ra h = \(\frac{{2.6\sqrt 6 }}{{(\sqrt {12} + \sqrt {24} )}} = 12 – 6\sqrt 2 \)