Giải Câu hỏi Hoạt động 2 trang 71 SGK Toán 9 Chân trời sáng tạo – Bài 2. Tứ giác nội tiếp. Gợi ý: Dựa vào tính chất của số đo góc nội tiếp bằng \(\frac{1}{2}\) số đo cung bị chắn.
Câu hỏi/Đề bài:
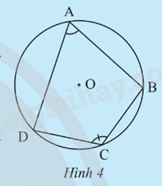
Cho tứ giác ABCD nội tiếp đường tròn (O) (Hình 4).
a) Chỉ ra các cung chắn bởi mỗi góc nội tiếp \(\widehat {DAB}\) và \(\widehat {DCB}\)
b) Tính tổng số đo của các cung vừa tìm được.
c) Nêu kết luận về tổng số đo của hai góc \(\widehat {DAB}\) và \(\widehat {DCB}\).
d) Có nhận xét gì về tổng số đo của hai góc đối diện còn lại của tứ giác ABCD?
Hướng dẫn:
– Dựa vào tính chất của số đo góc nội tiếp bằng \(\frac{1}{2}\) số đo cung bị chắn.
– Dựa vào tổng các góc của tứ giác bằng 360o.
Lời giải:
a) Góc \(\widehat {DAB}\) là góc nội tiếp chắn cung BD nhỏ.
Góc \(\widehat {DAB}\) là góc nội tiếp chắn cung BD lớn.
b) – Góc \(\widehat {DAB}\) là góc nội tiếp chắn cung BD nhỏ.
Suy ra \(\widehat {DAB} = \frac{1}{2}\) số đo cung BD nhỏ.
– Góc \(\widehat {DCB}\) là góc nội tiếp chắn cung BD lớn.
Suy ra \(\widehat {DCB} = \frac{1}{2}\) số đo cung BD lớn.
Ta có \(\widehat {DAB} + \widehat {DCB} = \frac{1}{2}\) (số đo cung BD nhỏ + số đo cung BD lớn)
= \(\frac{1}{2}\).360o = 180o.
c) Tổng số đo của hai góc \(\widehat {DAB}\) và \(\widehat {DCB}\) bằng 180o.
d) Tổng số đo của hai góc đối diện còn lại của tứ giác ABCD là 180o
(vì 360o – 180o = 180o).