Bài tập 4 trang 80 Toán 9 tập 2 – Chân trời sáng tạo: Cho đường tròn (O; R). a) Vẽ hình tam giác đều, hình vuông, hình lục giác đều có các đỉnh nằm trên (O; R)

Đề bài/câu hỏi:

Cho đường tròn (O; R).

a) Vẽ hình tam giác đều, hình vuông, hình lục giác đều có các đỉnh nằm trên (O; R).

b) Tính các cạnh của các hình vừa vẽ theo R.

Hướng dẫn:

– Đọc kĩ dữ kiện đề bài để vẽ hình.

– Dựa vào: Đa giác lồi có các cạnh bằng nhau và các góc bằng nhau gọi là đa giác đều.

– Dựa vào đường tròn ngoại tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác và bán kính bằng \(\frac{{a\sqrt 3 }}{3}\).

– Dựa vào: Đường tròn ngoại tiếp hình chữ nhật, hình vuông có tâm là giao điểm của hai đường chéo và có bán kính bằng nửa đường chéo.

Lời giải:

a)

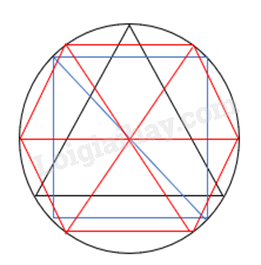
b) Tam giác đều nội tiếp đường tròn nên ta có:

R = \(\frac{{a\sqrt 3 }}{3}\) (a là độ dài cạnh tam giác đều)

Suy ra a = \(\frac{{3R}}{{\sqrt 3 }} = R\sqrt 3 \)

Hình vuông nội tiếp đường tròn nên ta có:

\(R = \frac{d}{2}\) (d là đường chéo của hình vuông)

Suy ra d = 2R. Gọi x là độ dài cạnh hình vuông hay \(\sqrt {{x^2} + {x^2}} = 2R\) suy ra \(x\sqrt 2 = 2R\)

Hay x = \(\frac{{2R}}{{\sqrt 2 }} = R\sqrt 2 \)

Trong lục giác đều có khoảng cách từ tâm đến các đỉnh là bằng nhau (= R); các góc ở tâm đều bằng 60^o nên lục giác đều gồm 6 tam giác đều.

Suy ra độ dài cạnh của lục giác đều là R.