Dựa vào: Đa giác lồi có các cạnh bằng nhau và các góc bằng nhau gọi là đa giác đều. Lời giải Giải bài tập 2 trang 79 SGK Toán 9 tập 2 – Chân trời sáng tạo – Bài 3. Đa giác đều và phép quay. Cho đa giác đều 9 cạnh có tâm O và AB, BC là hai cạnh đa giác (Hình 12)….
Đề bài/câu hỏi:
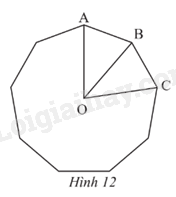
Cho đa giác đều 9 cạnh có tâm O và AB, BC là hai cạnh đa giác (Hình 12).
a) Tìm số đo các góc \(\widehat {AOB}\), \(\widehat {ABO}\), \(\widehat {ABC}\).
b) Tìm các phép quay biến đa giác thành chính nó.
Hướng dẫn:
– Dựa vào: Đa giác lồi có các cạnh bằng nhau và các góc bằng nhau gọi là đa giác đều.
– Dựa vào phép quay thuận chiều \({\alpha ^o}({0^o} < {\alpha ^o} < {360^o})\) tâm O giữ nguyên điểm O, biến điểm M khác điểm O thành điểm M’ thuộc đường tròn (O;OM) sao cho khi tia OM quay thuận chiều kim đồng hồ đến tia OM’ thì điểm M tạo nên cung MM’ có số đo \({\alpha ^o}\). Định nghĩa tương tự cho phép quay ngược chiều \({\alpha ^o}\) tâm O. Phép quay \({0^o}\) hay \({360^o}\) giữ nguyên mọi điểm.
Lời giải:
a) 9 đỉnh của đa giác chia đường tròn thành 9 phần bằng nhau, số đo mỗi cung là: 360o : 9 = 40o.
Vì \(\widehat {AOB}\) là góc nội tiếp chắn cung AB nhỏ
Suy ra \(\widehat {AOB} = {40^o}\).
Do OA = OB = R nên tam giác AOB cân tại O
Suy ra \(\widehat {OAB} = \widehat {OBA} = \frac{{{{180}^o} – \widehat {AOB}}}{2} = {70^o}\).
Tương tự, ta có \(\widehat {COB} = {40^o}\).
Suy ra \(\widehat {OBC} = \widehat {OCB} = \frac{{{{180}^o} – \widehat {BOC}}}{2} = {70^o}\)
Ta có \(\widehat {ABC} = \widehat {OBA} + \widehat {OBC} = {70^o} + {70^o} = {140^o}\).
b) Các phép quay biến đa giác thành chính nó là các phép quay 40o, 80o, 120o, 160o, 200o, 240o, 280o, 320o hoặc 360o tâm O cùng chiều hay ngược chiều kim đồng hồ.