Chứng minh \(\Delta \)CHB \(\backsim \) \(\Delta \)HDB (g. g) và \(\Delta \)FHA \(\backsim \) \(\Delta \)HEA (g. Phân tích, đưa ra lời giải Giải bài tập 15 trang 105 SGK Toán 9 tập 1 – Chân trời sáng tạo – Bài tập cuối chương 5. Hải đăng Kê Gà tọa lạc tại xã Tân Thành, huyên Hàm Thuận Nam, tỉnh Bình Thuận….
Đề bài/câu hỏi:
Hải đăng Kê Gà tọa lạc tại xã Tân Thành, huyên Hàm Thuận Nam, tỉnh Bình Thuận. Biết ngọn hải đăng cao 65 m so với mặt nước biển. Với khoảng cách bao nhiêu kilomet thì người quan sát trên tàu bắt đầu trông thấy ngọn của hải đăng này?
Cho biết mắt người quan sát ở độ cao 5 m so với mực nước biển và bán kính Trái Đất gần bằng 6400 km.

Hướng dẫn:
Chứng minh \(\Delta \)CHB \(\backsim \) \(\Delta \)HDB (g.g) và \(\Delta \)FHA \(\backsim \) \(\Delta \)HEA (g.g) rồi suy ra tỉ số đồng dạng để tính.
Lời giải:
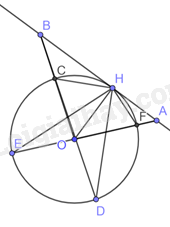
BO cắt đường tròn (O) tại 2 điểm C và D. Điểm C nằm giữa B và O.
Người quan sát đứng tại vị trí tàu nhìn xa tối đa trên mặt biển một đoạn tương ứng HB.
Xét tam giác BHC và tam giác BHD có:
\(\widehat B\) chung
\(\widehat {CBH} = \widehat {HDB}\) (cùng chắn cung HC)
Vậy \(\Delta \)CHB \(\backsim \) \(\Delta \)HDB (g.g)
Suy ra \(\frac{{BH}}{{BD}} = \frac{{CB}}{{HB}}\)
HB2 = CB.BD
HB2 = CB.(BC + CD)
HB2 = CB.(BC + 2R)
Thay số, ta có:
HB2 = 0,005.(0,005 + 2.6400) (CB = 5 m = 0,005 km)
Suy ra HB \( \approx \) 8 km
Ta có OA cắt đường tròn (O) tại E và F. Điểm F nằm giữa O và A.
Chứng minh tương tự trên, ta có:
Vậy \(\Delta \)FHA \(\backsim \) \(\Delta \)HEA (g.g)
Suy ra \(\frac{{AH}}{{AE}} = \frac{{FA}}{{HA}}\)
AH2 = FA.AE
AH2 = FA.(FA+EF)
AH2 = FA.(FA + 2R)
Thay số, ta có:
AH2 = 0,0065.(0,0065 + 2.6400) (FA = 65 m = 0,0065 km)
Suy ra AH \( \approx \) 29 km
Vậy AB = HA + HB = 29 + 8 \( \approx \) 37 km.