Giải Câu hỏi Luyện tập 1 trang 77 SGK Toán 9 Cánh diều – Bài 1. Tỉ số lượng giác của góc nhọn. Tham khảo: Dựa vào định lí Pythagore để tính cạnh \(NP\).
Câu hỏi/Đề bài:
Cho tam giác \(MNP\) vuông tại \(M,MN = 3cm,MP = 4cm\). Tính độ dài cạnh \(NP\) và các tỉ số lượng giác của góc \(P\).
Hướng dẫn:
+ Dựa vào định lí Pythagore để tính cạnh \(NP\).
+ Dựa vào kiến thức đã học về tỉ số lượng giác để tính các tỉ số lượng giác của góc \(P\).
Lời giải:
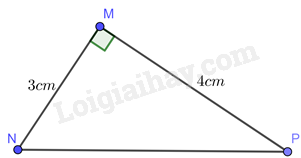
Xét tam giác \(MNP\) vuông tại \(M\), ta có:
\(NP = \sqrt {{3^2} + {4^2}} = \sqrt {25} = 5\left( {cm} \right)\)
Tam giác \(MNP\) vuông tại \(M\) nên:
+ \(\sin \widehat P = \frac{{MN}}{{NP}} = \frac{3}{5}.\)
+ \(\cos \widehat P = \frac{{MP}}{{NP}} = \frac{4}{5}.\)
+ \(\tan \widehat P = \frac{{MN}}{{MP}} = \frac{3}{4}.\)
+ \(\cot \widehat P = \frac{{MP}}{{MN}} = \frac{4}{3}.\)