Lời giải Câu hỏi Luyện tập 1 trang 107 SGK Toán 9 Cánh diều – Bài 3. Tiếp tuyến của đường tròn. Hướng dẫn: Dựa vào kiến thức vừa học để chứng minh.
Câu hỏi/Đề bài:
Cho ba điểm \(A,B,C\) thẳng hàng, trong đó \(B\) nằm giữa \(A\) và \(C\). Đường tròn \(\left( O \right)\) tiếp xúc với đường thẳng \(AB\) tại điểm \(C\). Chứng minh: \(A{O^2} + B{C^2} = B{O^2} + A{C^2}\).
Hướng dẫn:
Dựa vào kiến thức vừa học để chứng minh.
Lời giải:
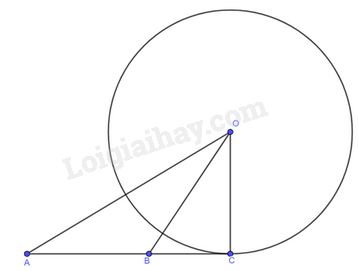
Vì đường thẳng \(AB\) tiếp xúc với đường tròn \(\left( O \right)\) tại \(C\) nên \(OC \bot AB\). Suy ra tam giác \(OBC\) vuông tại \(C\), tam giác \(OAC\) vuông tại C.
Áp dụng định lý Pythagore vào tam giác \(OAC\) vuông tại \(C\), ta có:
\(O{A^2} = O{C^2} + A{C^2} \Rightarrow O{C^2} = O{A^2} – A{C^2}\,\,\left( 1 \right)\).
Áp dụng định lý Pythagore vào tam giác \(OBC\) vuông tại \(C\), ta có:
\(O{B^2} = O{C^2} + B{C^2} \Rightarrow O{C^2} = O{B^2} – B{C^2}\,\,\,\left( 2 \right)\).
Từ (1) và (2) suy ra \(O{A^2} – A{C^2} = O{B^2} – B{C^2} \Rightarrow O{A^2} + B{C^2} = O{B^2} + A{C^2}\).