Sử dụng tính chất tam giác cân, định lí Pythagore để tính chiều cao cây. Giải và trình bày phương pháp giải Giải bài tập 8 trang 54 SGK Toán 9 tập 1 – Cánh diều – Bài 1. Căn bậc hai và căn bậc ba của số thực. Giông bão thổi mạnh, một cây bị gãy gập xuống làm ngọn cây chạm đất và tạo với phương năm…
Đề bài/câu hỏi:
Giông bão thổi mạnh, một cây bị gãy gập xuống làm ngọn cây chạm đất và tạo với phương năm ngang một góc \(45^\circ \) (minh họa ở Hình 3). Người ta đo được khoảng cách từ chỗ ngọn cây chạm đất đến gốc cây là \(4,5m\). Giả sử cây mọc vuông góc với mặt đất, hãy tính chiều cao của cây đó theo đơn vị mét (làm tròn kết quả đến hàng phần mười).
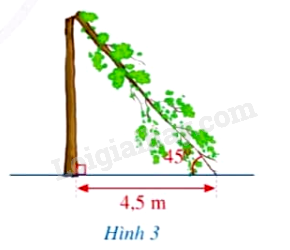
Hướng dẫn:
Sử dụng tính chất tam giác cân, định lí Pythagore để tính chiều cao cây.
Lời giải:
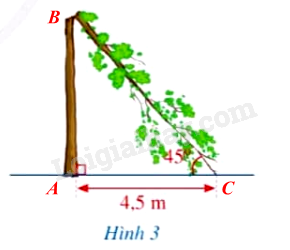
Gọi các điểm biểu diễn như hình vẽ.
Xét tam giác ABC vuông tại A có \(\widehat C = 45^\circ\) nên tam giác ABC vuông cân tại A.
Suy ra AB = AC = 4,5m.
Chiều cao phần ngọn bị gãy BC là: \(BC = \sqrt{AB^2+AC^2} = \sqrt{4,5^2 + 4,5^2} = \frac{9\sqrt2}{2} \approx 6,4(m)\)
Vậy chiều cao của cây là: \(AB + BC \approx 4,5 +6,4 = 10,9 (m)\)