Kết hợp với các kiến thức hình học cùng phép tính của căn thức để giải bài toán. Phân tích, đưa ra lời giải Giải bài tập 7 trang 60 SGK Toán 9 tập 1 – Cánh diều – Bài 2. Một số phép tính về căn bậc hai của số thực. Cho tam giác đều ABC có độ dài cạnh a….
Đề bài/câu hỏi:
Cho tam giác đều ABC có độ dài cạnh a. Tính độ dài đường cao AH của tam giác ABC theo a.
Hướng dẫn:
Kết hợp với các kiến thức hình học cùng phép tính của căn thức để giải bài toán
Lời giải:
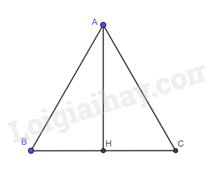
Do AH là đường cao của tam giác đều ABC.
Suy ra AH đồng thời là đường trung tuyến của tam giác ABC.
Suy ra H là trung điểm của BC.
Suy ra \(HB = HC = \frac{1}{2}BC = \frac{1}{2}a\).
Xét tam giác AHB vuông tại H có:
\(A{H^2} + H{B^2} = A{B^2}\) (Định lý Py – ta – go)
\(\begin{array}{l}A{H^2} + {\left( {\frac{a}{2}} \right)^2} = {a^2}\\A{H^2} = {a^2} – {\left( {\frac{a}{2}} \right)^2} = {a^2} – \frac{{{a^2}}}{4} = \frac{{4{a^2}}}{4} – \frac{{{a^2}}}{4} = \frac{{3{a^2}}}{4}\\AH = \frac{{a\sqrt 3 }}{2}.\end{array}\)
Vậy \(AH = \frac{{a\sqrt 3 }}{2}\).