Dựa vào tỉ số lượng giác để giải bài toán. Hướng dẫn cách giải/trả lời Giải bài tập 4 trang 92 SGK Toán 9 tập 1 – Cánh diều – Bài tập cuối chương 4. Một người đứng ở vị trí (B) trên bờ sông muốn sử dụng la bàn để ước lượng khoảng cách…
Đề bài/câu hỏi:
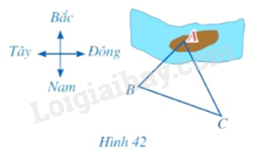
Một người đứng ở vị trí \(B\) trên bờ sông muốn sử dụng la bàn để ước lượng khoảng cách từ vị trí đó đến một vị trí \(A\) ở trên một cù lao giữa dòng sông. Người đó đã làm như sau:
– Sử dụng la bàn, xác định được phương \(BA\) lệch với phương Nam – Bắc về hướng Đông \(52^\circ \).
– Người đó di chuyển đến vị trí \(C\), cách \(B\) một khoảng là 187m. Sử dụng la bàn, xác định được phương \(CA\) lệch với phương Nam – Bắc về hướng Tây \(27^\circ \); \(CB\) lệch với phương Nam – Bắc về hướng Tây \(70^\circ \) (Hình 42).
Em hãy giúp người đó tính khoảng cách \(AB\) từ những dữ liệu trên (làm tròn kết quả đến hàng đơn vị của mét).
Hướng dẫn:
Dựa vào tỉ số lượng giác để giải bài toán.
Lời giải:
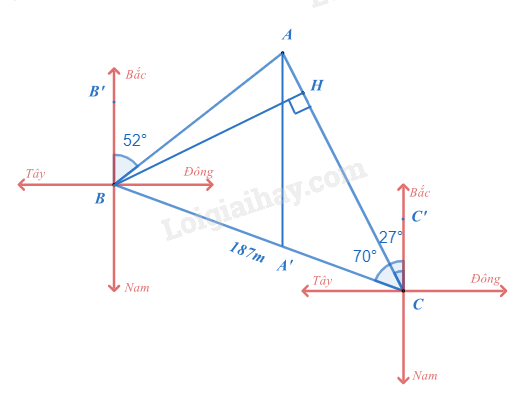
Lấy B’B, C’C là các đường thẳng biểu diễn phương Nam – Bắc như hình vẽ.
Theo bài ra ta có \(\widehat {B’BA} = 52^\circ ,\widehat {C’CA} = 27^\circ ,\widehat {C’CB} = 70^\circ \) suy ra \(\widehat {ACB} = \widehat {C’CB} – \widehat {C’CA} = 70^\circ – 27^\circ = 43^\circ \).
Kẻ AA’ ( \(A’ \in BC\)) song song với phương Nam – Bắc, khi đó \(AA’//BB’//CC’\).
Vì \(AA’//BB’//CC’\) nên ta có \(\widehat {B’BA} = \widehat {BAA’} = 52^\circ \) (hai góc so le trong) và \(\widehat {A’AC} = \widehat {C’CA} = 27^\circ \) suy ra \(\widehat {BAC} = \widehat {BAA’} + \widehat {A’AC} = 52^\circ + 27^\circ = 79^\circ \).
Kẻ \(BH \bot AC\left( {H \in AC} \right)\).
Xét \(\Delta BHC\) vuông tại H có: \(\sin C = \frac{{BH}}{{BC}}\) suy ra \(BH = \sin C.BC = \sin 43^\circ .187 \approx 128\left( m \right)\).
Xét \(\Delta BAH\) vuông tại H có: \(\sin A = \frac{{BH}}{{BA}}\) suy ra \(BA = \frac{{BH}}{{\sin A}} \approx \frac{{128}}{{\sin 79^\circ }} \approx 130\left( m \right)\)
Vậy khoảng cách AB là khoảng 130m.