Thay \(y = 125, t = 5\) vào hàm số \(y = a{t^2}\) để tìm a. Gợi ý giải Giải bài tập 4 trang 51 SGK Toán 9 tập 2 – Cánh diều – Bài 1. Hàm số y = ax² (a ≠ 0). Cho hàm số \(y = a{t^2}\) biểu thị quãng đường (đơn vị:…
Đề bài/câu hỏi:
Cho hàm số \(y = a{t^2}\) biểu thị quãng đường (đơn vị: mét) mà một chiếc xe đua đi được trong khoảng thời gian t (giây). Giả sử một chiếc xe đua đi được 125m sau khoảng thời gian là 5 giây.
a) Tìm hệ số a.
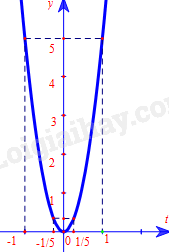
b) Vẽ đồ thị của hàm số.
Hướng dẫn:
a) Thay \(y = 125,t = 5\) vào hàm số \(y = a{t^2}\) để tìm a.
b) Xác định 5 điểm thuộc đồ thị hàm số, sau đó vẽ đường cong parabol đi qua 5 điểm đó.
Lời giải:
a) Thay \(y = 125,t = 5\) vào hàm số \(y = a{t^2}\) ta được:
\(125 = a{.5^2} \Leftrightarrow a = 5\)
Hàm số có dạng \(y = 5{t^2}\).
b) Ta có bảng:
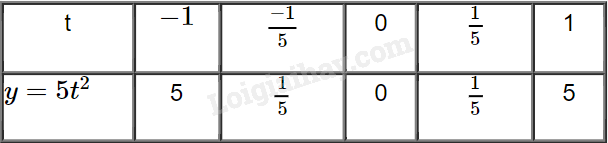
Đồ thị hàm số \(y = 5{t^2}\) là một parabol đi qua 5 điểm \(\left( { – 1;5} \right),(\frac{{ – 1}}{5};\frac{1}{5});\left( {0;0} \right),\left( {\frac{1}{5};\frac{1}{5}} \right),\left( {1;5} \right)\)