Dựa vào tính chất tiếp tuyến để chứng minh. Hướng dẫn giải Giải bài tập 3 trang 110 SGK Toán 9 tập 1 – Cánh diều – Bài 3. Tiếp tuyến của đường tròn. Cho đường tròn \(\left( O \right)\) và điểm \(M\) nằm ngoài đường tròn. Hai đường thẳng thẳng \(c,d\…
Đề bài/câu hỏi:
Cho đường tròn \(\left( O \right)\) và điểm \(M\) nằm ngoài đường tròn. Hai đường thẳng thẳng \(c,d\) đi qua \(M\) lần lượt tiếp xúc với \(\left( O \right)\) tại \(A,B\). Tia phân giác của góc \(MAB\) cắt \(MO\) tại \(I\). Chứng minh điểm \(I\) cách đều ba đường thẳng \(MA,MB\) và \(AB\).
Hướng dẫn:
Dựa vào tính chất tiếp tuyến để chứng minh.
Lời giải:
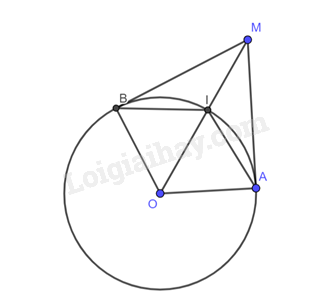
Do \(MA,MB\) là tiếp tuyến của đường tròn \(\left( O \right)\) nên \(MO\) là tia phân giác của \(\widehat {AMB}\) hay \(MI\) là tia phân giác của \(\widehat {AMB}\).
Xét tam giác \(AMB\) có:
\(BI\) là tia phân giác của góc \(MAB\);
\(MI\) là tia phân giác của góc \(AMB\).
Suy ra \(I\) là giao điểm của 3 đường phân giác tam giác \(AMB\).
Vậy \(I\) cách đều \(MA,MB,AB\).