Dựa vào các mối liên hệ giữa tỉ số lượng giác và các cạnh để giải bài toán. Phân tích và giải Giải bài tập 2 trang 86 SGK Toán 9 tập 1 – Cánh diều – Bài 2. Một số hệ thức về cạnh và góc trong tam giác vuông. Cho tam giác (ABC) có đường cao (AH = 6cm,widehat B = 40^circ ,widehat C = 35^circ )….
Đề bài/câu hỏi:
Cho tam giác \(ABC\) có đường cao \(AH = 6cm,\widehat B = 40^\circ ,\widehat C = 35^\circ \). Tính độ dài các đoạn thẳng \(AB,BH,AC,BC\) (làm tròn kết quả đến hàng phần mười của centimét).
Hướng dẫn:
Dựa vào các mối liên hệ giữa tỉ số lượng giác và các cạnh để giải bài toán.
Lời giải:
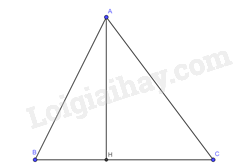
Xét tam giác \(ABH\) vuông tại \(H\), ta có:
+) \(AB = \frac{{AH}}{{\sin 40^\circ }} = \frac{6}{{\sin 40^\circ }} \approx 9,3\left( {cm} \right)\).
+) \(BH = \frac{{AH}}{{\tan 40^\circ }} = \frac{6}{{\tan 40^\circ }} \approx 7,2\left( {cm} \right)\).
Xét tam giác \(AHC\) vuông tại \(H\), ta có:
+) \(AC = \frac{{AH}}{{\sin 35^\circ }} = \frac{6}{{\sin 35^\circ }} \approx 10,5\left( {cm} \right)\).
+) \(CH = \frac{{AH}}{{\tan 35^\circ }} = \frac{6}{{\tan 35^\circ }} \approx 8,6\left( {cm} \right)\).
Ta có: \(BC = BH + HC \approx 7,2 + 8,6 \approx 15,8\left( {cm} \right)\).