Thay từng giá trị của x vào hàm số \(y = \frac{1}{3}{x^2}\) để tìm được y tương ứng. Gợi ý giải Giải bài tập 2 trang 51 SGK Toán 9 tập 2 – Cánh diều – Bài 1. Hàm số y = ax² (a ≠ 0). Cho hàm số \(y = \frac{1}{3}{x^2}\). a) Tìm giá trị của y tương ứng với giái trị của x trong…
Đề bài/câu hỏi:
Cho hàm số \(y = \frac{1}{3}{x^2}\).
a) Tìm giá trị của y tương ứng với giái trị của x trong bảng sau:

b) Dựa vào bảng giá trị trên, vẽ đồ thị của hàm số đó.
c) Tìm những điểm thuộc đồ thị của hàm số có hoành độ lần lượt bằng -6; 10.
d) Tìm những điểm thuộc đồ thị của hàm số có tung độ bằng 27.
Hướng dẫn:
a) Thay từng giá trị của x vào hàm số \(y = \frac{1}{3}{x^2}\) để tìm được y tương ứng.
b) Thay lần lượt \(x = – 6,x = 10\)vào hàm số để tìm được tung độ tương ứng.
c) Thay\(y = 27\) hàm số để tìm được các hoành độ tương ứng.
Lời giải:
a) Ta có bảng giá trị sau:
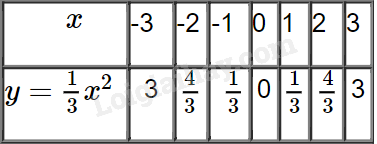
b) Thay \(x = – 6\) vào hàm số \(y = \frac{1}{3}{x^2}\) ta được:
\(y = \frac{1}{3}{( – 6)^2} \Leftrightarrow y = 12\).
Ta có điểm (-6; 12) thuộc đồ thị hàm số \(y = \frac{1}{3}{x^2}\).
Thay \(x = 10\) vào hàm số \(y = \frac{1}{3}{x^2}\) ta được:
\(y = \frac{1}{3}{(10)^2} \Leftrightarrow y = \frac{{100}}{3}\).
Ta có điểm \(\left( {10;\frac{{100}}{3}} \right)\) thuộc đồ thị hàm số \(y = \frac{1}{3}{x^2}\).
c) Thay \(y = 27\) vào hàm số \(y = \frac{1}{3}{x^2}\) ta được:
\(27 = \frac{1}{3}{x^2} \Leftrightarrow {x^2} = 81 \Leftrightarrow x = \pm 9\).
Ta có điểm \(\left( { – 9;27} \right),\left( {9;27} \right)\) thuộc đồ thị hàm số \(y = \frac{1}{3}{x^2}\).