Bước 1: Dựa vào mối quan hệ giữa 3 cạnh trong tam giác, ta có \(AB \ge O’A – O’B\), \(AO’ \ge O’O – OA\. Hướng dẫn giải Giải bài 7 trang 103 sách bài tập toán 9 – Cánh diều tập 1 – Bài 1. Đường tròn. Vị trí tương đối của hai đường tròn. Hai hòn đảo được xem như hai hình tròn có khoảng cách từ tâm hòn đảo này đến tâm hòn…
Đề bài/câu hỏi:
Hai hòn đảo được xem như hai hình tròn có khoảng cách từ tâm hòn đảo này đến tâm hòn đảo kia là khoảng 950 m. Biết rằng hòn đảo lớn có bán kính khoảng 500 m, còn đảo nhỏ có bán kính khoảng 300 m. Người ta cần xây dựng một cây cầu bắc từ đảo này sang đảo kia. Hãy chọn vị trí để xây cầu sao cho chiều dài cây cầu là ngắn nhất, khi đó tính chiều dài cây cầu.
Hướng dẫn:
Bước 1: Dựa vào mối quan hệ giữa 3 cạnh trong tam giác, ta có \(AB \ge O’A – O’B\), \(AO’ \ge O’O – OA\) (có trường hợp dấu “=” là do có thể xảy ra trường hợp 3 điểm thẳng hàng).
Bước 2: Cộng từng vế của 2 đẳng thức trên.
Bước 3: Tìm giá trị nhỏ nhất của AB và trường hợp dấu “=” xảy ra.
Lời giải:
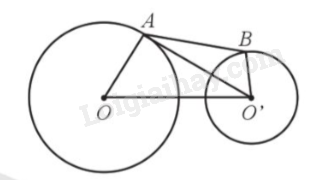
Khoảng cách từ tâm hòn đảo này đến tâm hòn đảo kia là \(OO’ = 950m\), bán kính đảo lớn \(OA = 500m\), bán kính đảo nhỏ \(OB = 300m\); chiều dài cây cầu là AB.
Xét 3 điểm O’. A, B ta có \(AB \ge O’A – O’B\)
Xét 3 điểm O, O’, A ta có \(AO’ \ge O’O – OA\)
Do đó \(AB – AO’ \ge O’A – O’B – O’O – OA\) hay \(AB \ge O’O – OA – O’B\)
hay \(AB \ge 950 – 500 – 300 = 150\)m.
Dấu “=” xảy ra khi 4 điểm O, A, B, O’ thẳng hàng theo thứ tự đó. Vậy ta nên đặt cây cầu trên đoạn nối tâm của 2 đảo thì cây cầu có chiều dài ngắn nhất là 150m.