Diện tích cần tìm = diện tích BCHI + diện tích LEFK – diện tích ADGJ b) Bước 1. Hướng dẫn cách giải/trả lời Giải bài 43 trang 74 sách bài tập toán 9 – Cánh diều tập 2 – Bài tập cuối Chương 7. Một biển báo giao thông có một phần dạng hình chữ thập với các kích thước x (cm),…
Đề bài/câu hỏi:
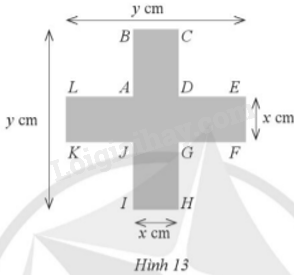
Một biển báo giao thông có một phần dạng hình chữ thập với các kích thước x (cm), y (cm) và \(y = x + 25,\) \(AL = AB = CD = DE = FG = GH = IJ = JK\) như hình 13.
a) Tính diện tích phần hình chữ thập của biển báo giao thông đó theo x.
b) Tìm x nếu diện tích phần hình chữ thập của biển báo giao thông đó là 975cm2.
Hướng dẫn:
a) Diện tích cần tìm = diện tích BCHI + diện tích LEFK – diện tích ADGJ
b) Bước 1: Lập phương trình thể hiện diện tích phần hình chữ thập.
Bước 2: Giải phương trình, đối chiếu điều kiện và kết luận.
Lời giải:
Điều kiện \(x > 0;y > 25\).
a) Diện tích hình chữ nhật BCHI là \(xy = x\left( {x + 25} \right) = {x^2} + 25x\) (m2)
Diện tích hình chữ nhật LEFK là \(xy = x\left( {x + 25} \right) = {x^2} + 25x\) (m2)
Diện tích hình vuông ADGJ là \({x^2}\) (m2)
Diện tích phần hình chữ thập là: \({x^2} + 25x + {x^2} + 25x – {x^2} = {x^2} + 50x\)(m2)
b) Vì diện tích phần hình chữ thập của biển báo giao thông đó là 975cm2 nên ta có:
\({x^2} + 50x = 975\), do đó \({x^2} + 50x – 975 = 0\)
Ta có \(\Delta ‘ = {25^2} – 1.\left( { – 975} \right) = 1600 > 0\) nên phương trình có 2 nghiệm phân biệt:
\({x_1} = \frac{{ – 25 – \sqrt {1600} }}{1} = – 65;{x_2} = \frac{{ – 25 + \sqrt {1600} }}{1} = 15\)
Ta thấy \({x_1} = – 65\) không thỏa mãn điều kiện; \({x_2} = 15\) thỏa mãn điều kiện.
Vậy \(x = 15\).