Giải hệ gồm 2 phương trình trên ta tìm được độ dài cạnh đáy của mỗi hình chóp. Phân tích và giải Giải bài 36 trang 23 sách bài tập toán 9 – Cánh diều tập 1 – Bài tập cuối Chương 1. Ở Hình 5, cho hai hình chóp tứ giác đều S.ABCD và S’….
Đề bài/câu hỏi:
Ở Hình 5, cho hai hình chóp tứ giác đều S.ABCD và S’.A’B’C’D’ có cùng chiều cao SH= S’H = 30 cm. Thể tích của hình chóp S.ABCD nhỏ hơn thể tích của hình chóp S’A’B’C’D’ là 240 cm3. Tính độ dài cạnh đáy của mỗi hình chóp, biết \(A’B’ – AB = 2\)cm.
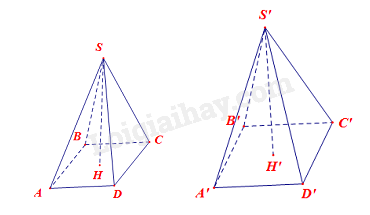
Hướng dẫn:

Giải hệ gồm 2 phương trình trên ta tìm được độ dài cạnh đáy của mỗi hình chóp.
Lời giải:
Ta có AB và A’B’ lần lượt là độ dài cạnh đáy của hình chóp tứ giác đều S.ABCD và S’.A’B’C’D’.
Theo đề bài ta có \(A’B’ – AB = 2\).
Thể tích hình chóp S.ABCD là \(\frac{1}{3}.A{B^2}.30\) cm3 và hình chóp S’.A’B’C’D’ là \(\frac{1}{3}.A’B{‘^2}.30\) cm3.
Do thể tích của hình chóp S.ABCD nhỏ hơn thể tích của hình chóp S’A’B’C’D’ là 240 cm3 nên ta có phương trình \(\frac{1}{3}.A’B{‘^2}.30 – \frac{1}{3}.A{B^2}.30 = 240\) hay \(A’B{‘^2} – A{B^2} = 24\).
Ta lập được hệ phương trình \(\left\{ \begin{array}{l}A’B’ – AB = 2\left( 1 \right)\\A’B{‘^2} – A{B^2} = 24\left( 2 \right)\end{array} \right.\)
Từ (1) suy ra \(A’B’ = 2 + AB\) (3). Thế (3) vào (2) ta được:
\(\begin{array}{l}{\left( {2 + AB} \right)^2} – A{B^2} = 24\\4 + 4AB + A{B^2} – A{B^2} – 24 = 0\\4AB = 20\\AB = 5\end{array}\)
Thay \(AB = 5\) vào (1) ta có \(A’B’ = 2 + 5 = 7\).
Vậy độ dài cạnh đáy của 2 hình chóp S.ABCD và S’.A’B’C’D’ lần lượt là 5cm và 7cm.