Sử dụng bất đẳng thức Cosi: a2 + b2 \( \ge \) 2ab (Dấu bằng xảy ra khi và chỉ khi a = b). Hướng dẫn trả lời Giải bài 33 trang 93 sách bài tập toán 9 – Cánh diều tập 2 – Bài tập cuối Chương 8. Cho đường tròn (I; r) cố định. Một tam giác ABC thay đổi,…
Đề bài/câu hỏi:
Cho đường tròn (I; r) cố định. Một tam giác ABC thay đổi, có chu vi bằng 16 cm và luôn ngoại tiếp đường tròn (I; r). Một tiếp tuyến song song với BC cắt các cạnh AB, AC lần lượt tại M và N. Tìm dộ dài BC để MN có độ dài lớn nhất.
Hướng dẫn:
Sử dụng bất đẳng thức Cosi: a2 + b2 \( \ge \) 2ab (Dấu bằng xảy ra khi và chỉ khi a = b).
Lời giải:
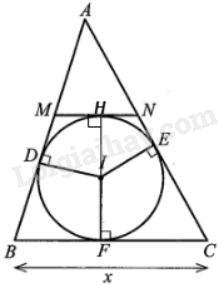
Giả sử đường tròn nội tiếp tam giác ABC tiếp xúc với các cạnh AB, BC, CA lần lượt tại D, F, E và BC = x.
Ta có MN // BC nên ∆AMN ᔕ ∆ABC.
Suy ra: \(\frac{{MN}}{{BC}} = \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\).
Theo tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{{MN}}{{BC}} = \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN + AM + AN}}{{BC + AB + AC}} = \frac{{chu{\rm{ }}vi\Delta AMN}}{{chu{\rm{ }}vi\Delta ABC}}\) (*)
Vì AD, AE là các tiếp tuyến của đường tròn (I; r) tại D, E nên AD = AE.
Tương tự, ta có BD = BF và CE = CF.
Do đó AD + AE = AB – BD + AC – CE
= AB + AC – (BD + CE)
= AB + AC – (BF + CF)
= AB + AC – BC.
Gọi H là tiếp điểm của đường tròn (I; r) với MN.
Hai tiếp tuyến MD, MH của đường tròn (I; r) cắt nhau tại M nên MD = MH.
Tương tự ta có NE = NH.
Ta có:
Chu vi ∆AMN
= AM + AN + MN
= AD – MD + AE – NE + MN
= AD + AE – (MD + NE) + MN
= AD + AE – (MH + NH) + MN
= AD + AE – MN + MN
= AD + AE
= AB + AC – BC
= AB + AC + BC – 2BC
= Chu vi ∆ABC – 2x (với x = BC)
= 16 – 2x.
Từ (*) ta có: \(\frac{MN}{BC}=\frac{chu\text{ }vi\Delta AMN}{chu\text{ }vi\Delta ABC}\), hay \(\frac{{MN}}{x} = \frac{{16 – 2x}}{{16}}\).
Từ đó MN = \(\frac{{x(16 – 2x)}}{{16}} = \frac{{2x(8 – x)}}{{16}} = \frac{{4x(8 – x)}}{{32}} \le \frac{{{{\left[ {x + (8 – x)} \right]}^2}}}{{32}} = 2\).
Do đó, MN có độ dài lớn nhất bằng 2 cm khi x = 8 – x hay x = 4, tức là BC = 4 cm.