Áp dụng tỉ số lượng giác trong tam giác ABC để tính AC. Giải chi tiết Giải bài 29 trang 90 sách bài tập toán 9 – Cánh diều tập 1 – Bài tập cuối Chương 4. Một chiếc thang dài 6 m được đặt dựa vào tường và tạo với phương nằm ngang một góc 60⁰….
Đề bài/câu hỏi:
Một chiếc thang dài 6 m được đặt dựa vào tường và tạo với phương nằm ngang một góc 60⁰. Khi đó, khoảng cách giữa chân thang và chân tường là
A. 3m
B. \(3\sqrt 3 \)m
C. \(3\sqrt 2 \)m
D. \(2\sqrt 3 \)m
Hướng dẫn:
Áp dụng tỉ số lượng giác trong tam giác ABC để tính AC.
Lời giải:
Bài toán được mô tả như hình vẽ:
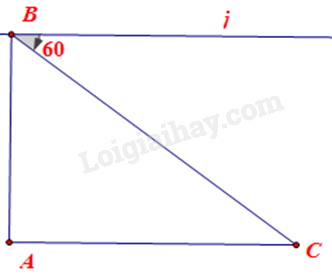
Độ dài thang là \(BC = 6\)m, khoảng cách giữa chân thang và chân tường là AC, góc tạo bởi thang và phương nằm ngang là \(\widehat {CBi} = 60^\circ \).
Do \(Bi//AC\) nên \(\widehat C = \widehat {CBi} = 60^\circ \).
Xét tam giác ABC vuông tại A, ta có:
\(\cos C = \frac{{AC}}{{BC}}\) nên \(AC = BC.\cos C = 6.\cos 60^\circ = 3\)m.
Đáp án A.