Chứng minh MNPQ là hình chữ nhật nội tiếp đường tròn nên bốn điểm M, N, P, Q cùng thuộc một đường tròn. Phân tích, đưa ra lời giải Giải bài 26 trang 92 sách bài tập toán 9 – Cánh diều tập 2 – Bài tập cuối Chương 8. Cho tứ giác ABCD có (widehat C + widehat D = {90^o}). Gọi M, N, P,…
Đề bài/câu hỏi:
Cho tứ giác ABCD có \(\widehat C + \widehat D = {90^o}\). Gọi M, N, P, Q lần lượt là trung điểm của AB, BD, DC, CA. Chứng minh bốn điểm M, N, P, Q cùng thuộc một đường tròn. Tìm tâm đường tròn đó.
Hướng dẫn:
Chứng minh MNPQ là hình chữ nhật nội tiếp đường tròn nên bốn điểm M, N, P, Q cùng thuộc một đường tròn.
Lời giải:
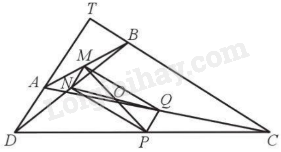
Gọi T là giao điểm của hai đường thẳng AD và CB. Vì \(\widehat {TDC} + \widehat {TCD} = {90^o}\) nên tam giác TCD vuông tại T.
Do MN là đường trung bình tam giác ABD nên MN // AD, MQ là đường trung bình của tam giác ABC nên MQ // BC.
Mặt khác, \(AD \bot BC\) suy ra \(MN \bot MQ\).
Chứng minh tương tự ta cũng có \(MN \bot NP,NP \bot PQ\). Suy ra MNPQ là hình chữ nhật.
Vậy bốn điểm M, N, P, Q cùng thuộc một đường tròn tâm O là giao điểm hai đường chéo MP và NQ.